Предмет: Математика,
автор: katyasweetsugar
Допоможіть будь-ласка
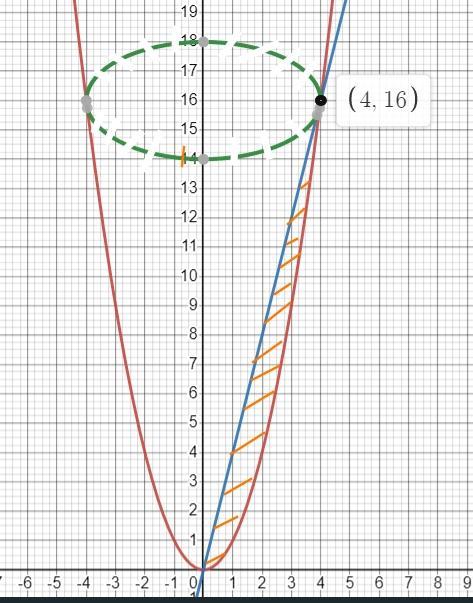
Обчислити об'єми тіл, утворених обертанням навколо осі ОY фігур, обмежених зазначеними лініями: y=x^2, 4x-y=0
Ответы
Автор ответа:
1
Ответ:
объем тела равен
Пошаговое объяснение:
Формула для вычисления объема тела, полученного вращением вокруг оси OY
Чертим графики функций y = x²; 4x - y = 0 (у = 4х)
Определяем пределы интегрирования
а = 4; b = 0
Определяем подынтегральную функцию
х² * 4x = 4x³
Считаем интеграл
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: СашаДубских
Предмет: Русский язык,
автор: каролина136в
Предмет: Русский язык,
автор: Плиз444
Предмет: Математика,
автор: andrey12346465566
Предмет: Химия,
автор: goryelovag