Предмет: Геометрия,
автор: pborysiuk
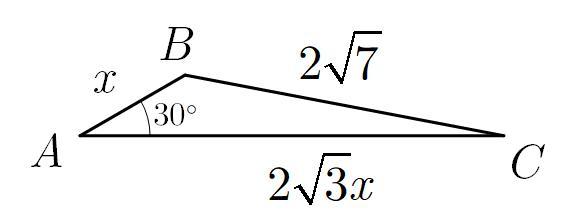
довжина сторони трикутника дорівнює 2корінь7 см, дві інші сторони утворюють утворюють кут 30 градусів, а їх довжини відносяться 1:2корінь3. Знайдіть найменшу із сторін трикутника
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Пускай в треугольнике
Тогда по теореме косинусов
Тогда стороны треугольника равны
Наименьшей из них является сторона
Приложения:
Автор ответа:
1
Вітаю
Відповідь: 2 см
Розв'язання завдання додаю
Приложения:

Похожие вопросы
Предмет: Другие предметы,
автор: Отличница1831
Предмет: Русский язык,
автор: Anyamironowa
Предмет: Русский язык,
автор: goodwar40
Предмет: Математика,
автор: Erikinooo
Предмет: Математика,
автор: Bomisrob