Предмет: Геометрия,
автор: pborysiuk
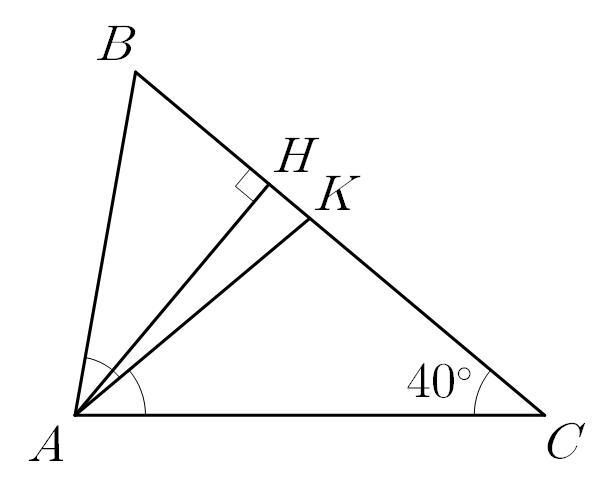
у трикутнику ABC кут C=40 градусів, кут A=80 градусів. Знайдіть кут між висотою AH і бісектрисою AK
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Угол треугольника равен
тогда в прямоугольном треугольнике
Но
Значит
Приложения:
Аноним:
мы где-то встречались же да?
не может обычный человек с улицы зарегистрироваться и за неделю профессионально оформлять решения в редакторе. с точками в конце формул и т д и т п
«Обычный человек с улицы» — это 5! :)
:)
Автор ответа:
0
Ответ:
10°
Объяснение:
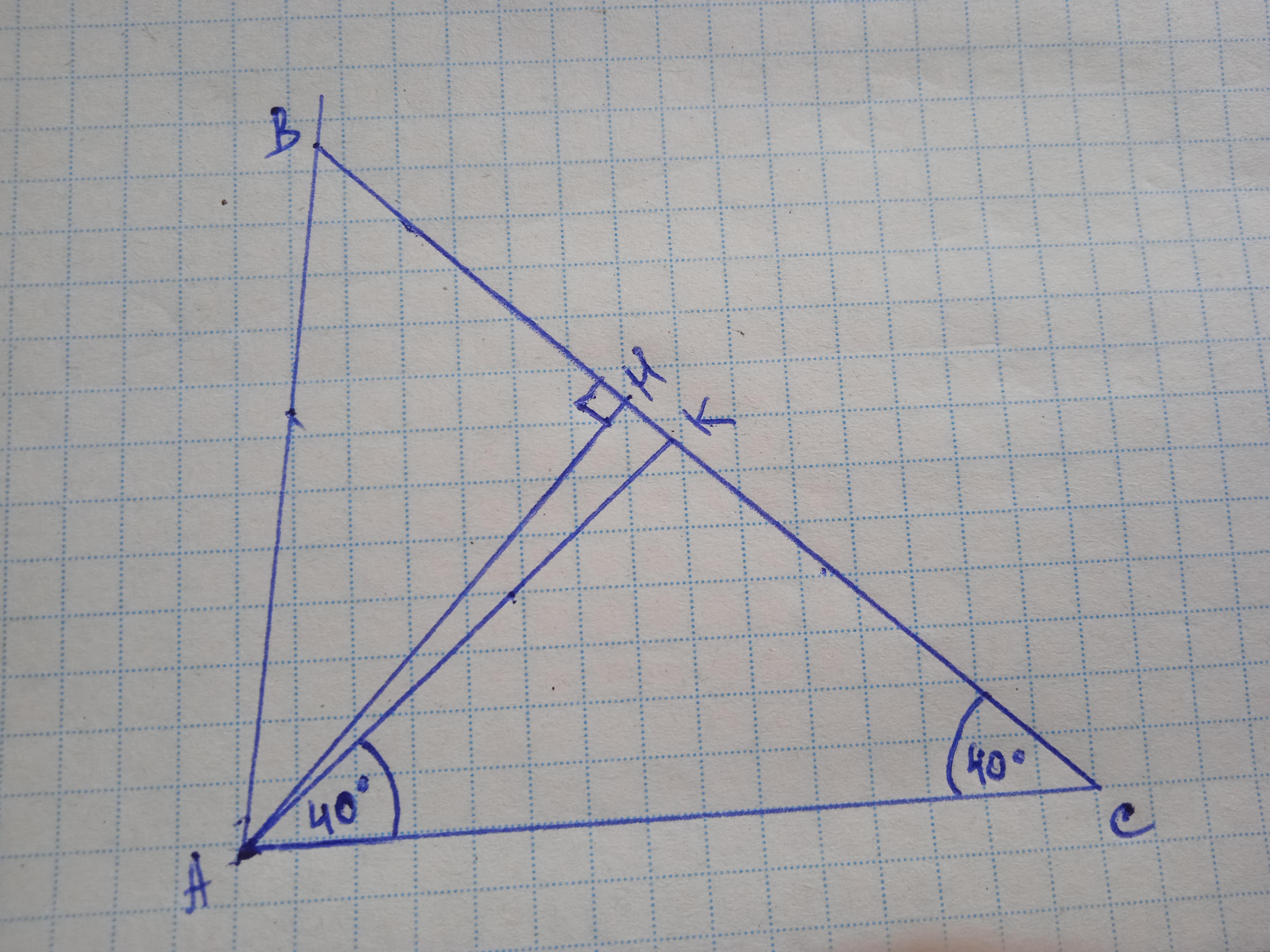
Дано: ΔАВС, ∠А=80°, ∠С=40°, АН - висота, АК - бісектриса.
∠КАН - ?
∠САК=∠ВАК=80:2=40° за визначенням бісектриси
∠АКС = 180-40-40=100°
∠АКВ=180-100=80°
ΔКАН - прямокутний
∠КАН=180-90-80=10°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: goodwar40
Предмет: Английский язык,
автор: Аноним
Предмет: Українська мова,
автор: skrip2018
Предмет: Математика,
автор: kuzmisereja2014