Question

Срочно!!! x^2=-2/x розв‘яжіть графічно рівняння

Answer 1

Ответ:

Ответ: $\displaystyle \bf -1\frac{1}{4}$

Объяснение:

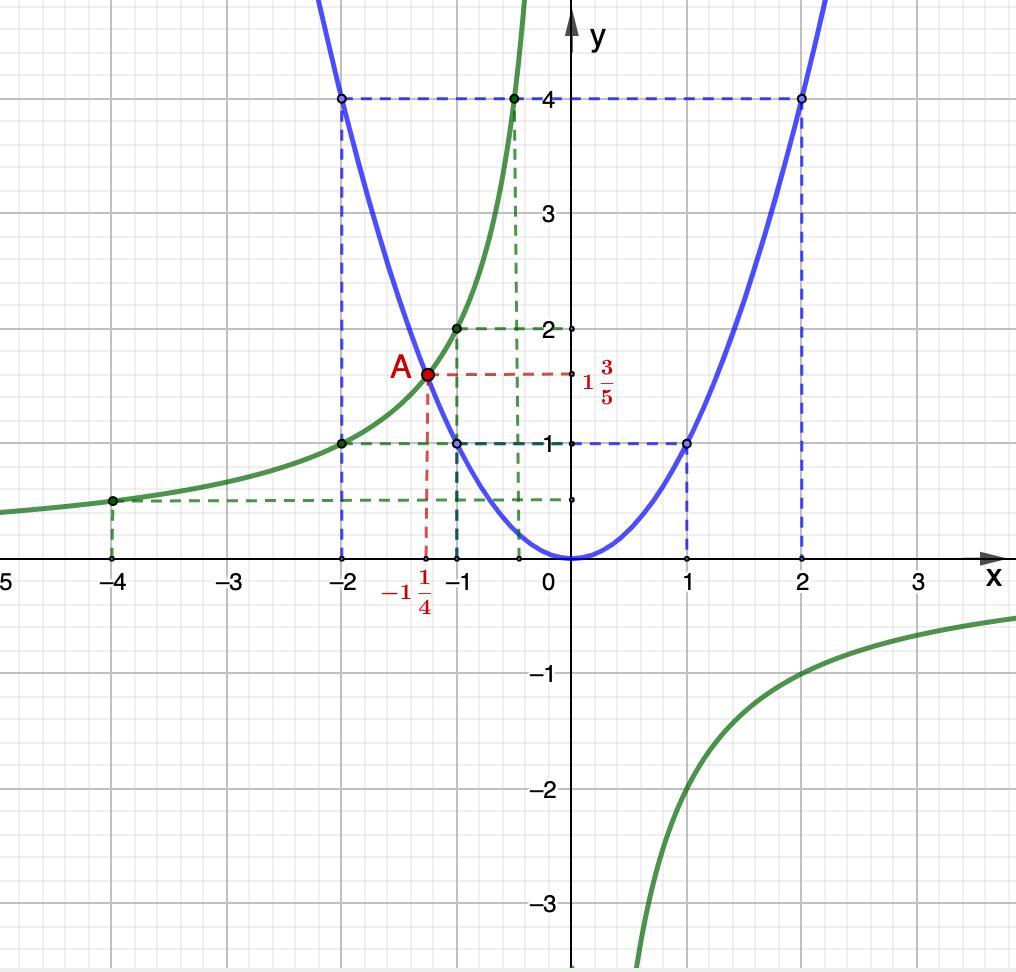
Решить уравнение графически:

$\displaystyle \bf x^2=-\frac{2}{x}$

Для решения данного уравнения необходимо построить два графика:

$\displaystyle \bf y=x^2\;\;\;\;\;u\;\;\;\;\;y=-\frac{2}{x}$

Абсциссы точек пересечения и будут решением данного уравнения.

1.

$\displaystyle \bf y=x^2$

- квадратичная функция, график - парабола, ветви вверх.

Построим график по точкам:

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c|c|c|c| }\cline{1-6}x& 0 & 1 & 2& -1 & -2 \\\cline{1-6}y& 0 & 1 & 4& 1 & 4 \\\cline{1-6}\end{array}$

2.

$\displaystyle \bf y=-\frac{2}{x}$

- функция обратной пропорциональности, график - гипербола, расположена во 2 и 4 четвертях.

Построим ветвь гиперболы:

$\displaystyle\arraycolsep=0.7em\begin{array}{ | c | c |c|c|c| }\cline{1-5}x& -\frac{1}{2} & -1 & -2& -4 \\\cline{1-5}y& 4 & 2 & 1& \frac{1}{2} \\\cline{1-5}\end{array}$

Вторая ветвь будет симметрична относительно начала координат.

Найдем точку пересечения графиков:

$\displaystyle \bf A\left(-1\frac{1}{4};\;1\frac{3}{5}\right)$

Ответ: $\displaystyle \bf -1\frac{1}{4}$