Предмет: Алгебра,
автор: katrineeeeeeeee721
Помогите пожалуйста! Прошу!
Приложения:
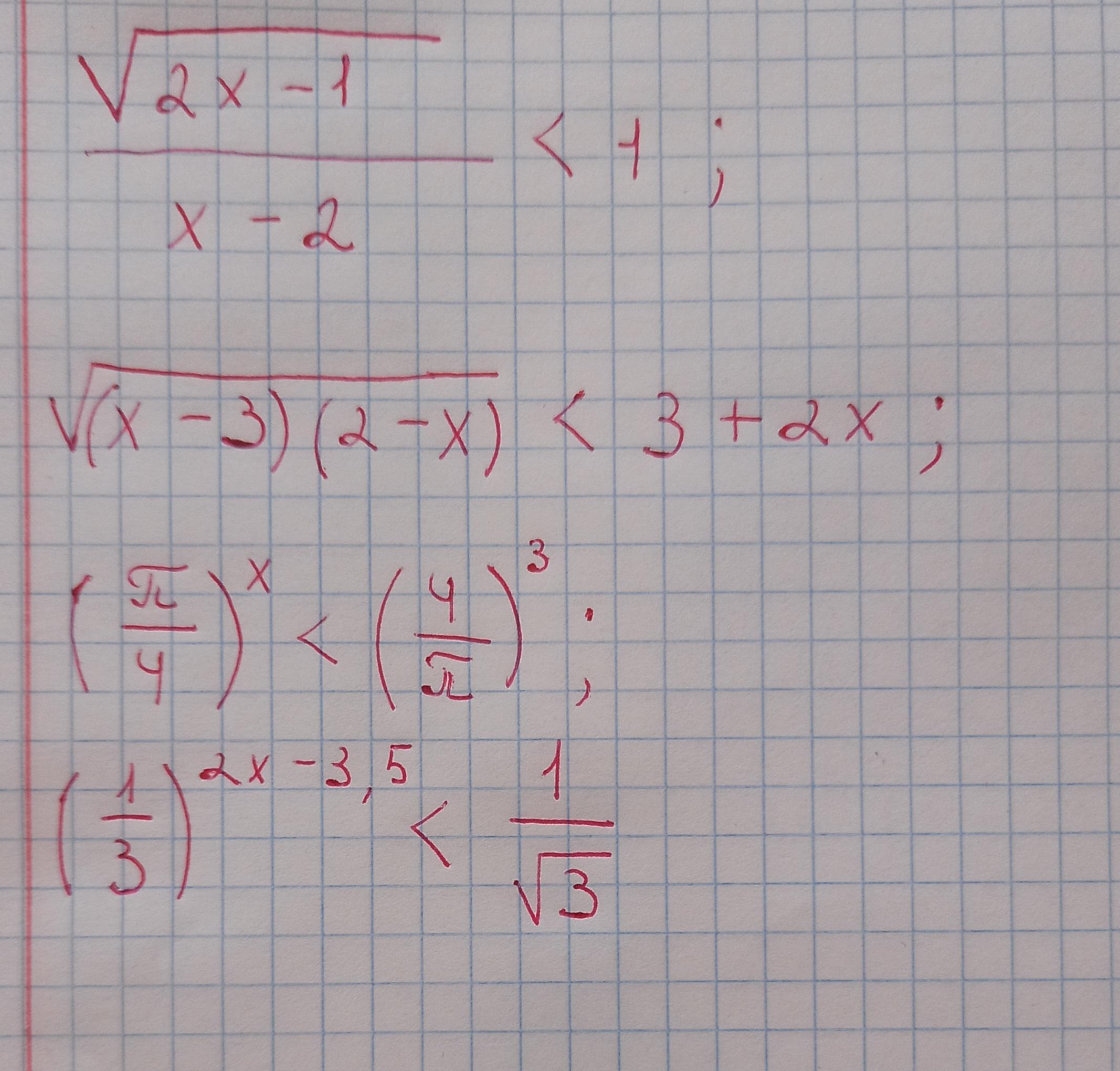
Ответы
Автор ответа:
1
Ответ:
Объяснение:
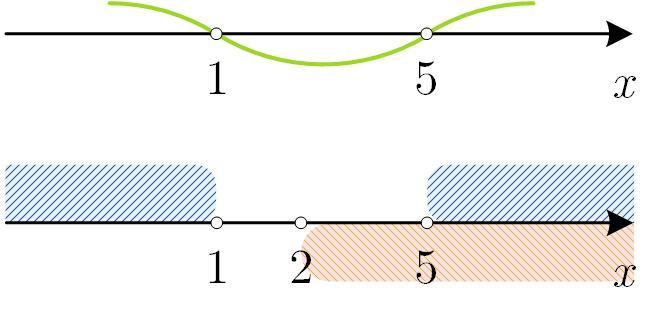
Решение неравенств и объединение промежутков в примерах 1–2 — см. рис.
1)
ОДЗ:
При левая сторона отрицательна, поэтому неравенство очевидно выполняется.
При возведем обе части в квадрат:
Так как знаменатель дроби при указанных значениях положительный, умножим на него обе части неравенства:
Так как то
Собирая обе части ответа, получаем
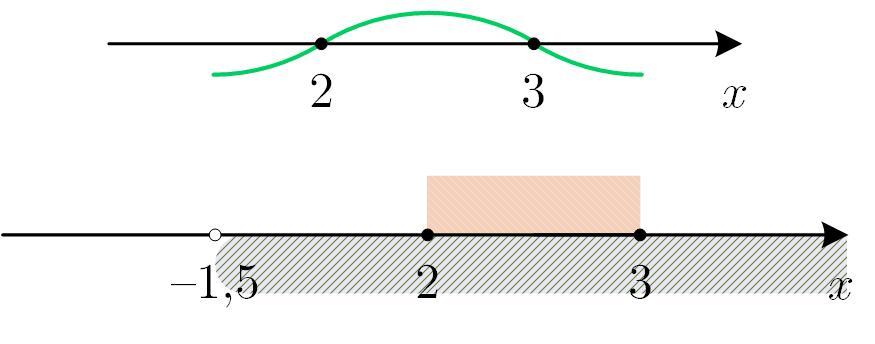
2)
Решение неравенств вида равносильно системе
то есть
Решение первого неравенства — второго —
Решим третье неравенство системы:
Последний квадратный трехчлен не имеет корней, а его старший коэффициент равен 5, что больше 0, поэтому при всех значениях
Значит
3)
Так как функция при
убывает, а
то
4)
Так как функция при
убывает, а
то
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: FES20061
Предмет: Окружающий мир,
автор: 20062006аля
Предмет: Английский язык,
автор: лариса212
Предмет: Русский язык,
автор: tamara0012
Предмет: История,
автор: SURUS140675