Предмет: Математика,
автор: muratmelikbayev30
34. (01-7-46) Найдите
Приложения:
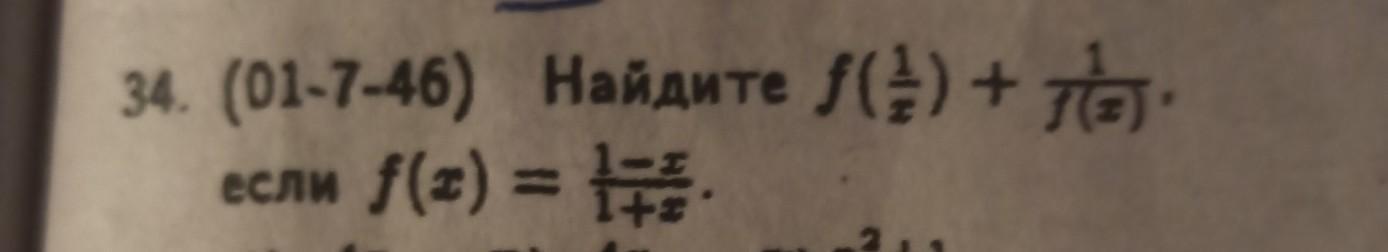
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Подставим в заданную функцию вместо аргумента x выражение
Тогда их сумма
muratmelikbayev30:
можешь посоветовать какие нибудь уроки ) ,это новая тема так что
Не силен, извини. Могу только сам преподать ;)
понятно (
Автор ответа:
0
Розв'язання #########
Приложения:

Похожие вопросы
Предмет: Қазақ тiлi,
автор: Sofya12341
Предмет: Другие предметы,
автор: Vanya1211qwerty
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: arabova37