Предмет: Математика,
автор: muratmelikbayev30
(00-9-55) Найдите область значений функции y=√x²-x
с объяснением
Ответы
Автор ответа:
0
Ответ:
Область значений функции [ 0; +∞)
Пошаговое объяснение:
Найти область значений функции
Найдем область определения данной функции
Так как арифметический квадратный корень определен на множестве неотрицательных чисел, то найдем область определения заданной функции, решив неравенство:
x=0 или x=1
Точки 0 и 1 разбивают числовую прямую на три промежутка. Определим знак на каждом промежутке ( во вложении)
Получим, что х ∈ (- ∞; 0]∪ [1; + ∞)
Тогда область определения D(y) =(- ∞; 0]∪ [1; + ∞)
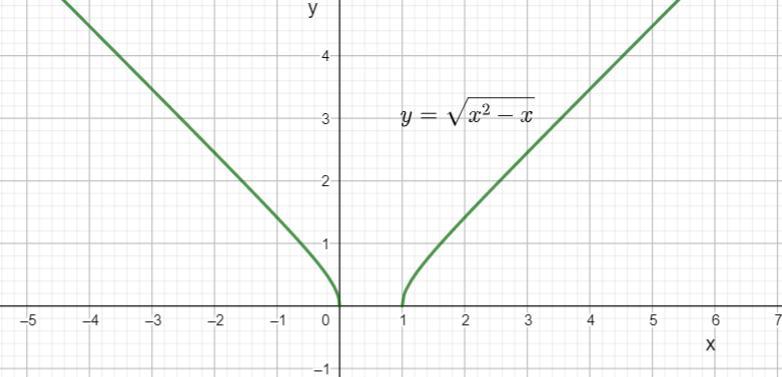
Построим на полученной области определения график заданной функции ( график во вложении)
Область значений функции - это множество значений , принимаемых переменной y.
По графику определяем, что
y ∈ [0; + ∞)
Значит, область значений функции [ 0; +∞)
Приложения:

antonovm:
вы решили другую задачу , в задании найти область значений
хотя возможно это плохой перевод
Похожие вопросы
Предмет: Русский язык,
автор: Лирик2106
Предмет: Русский язык,
автор: 3413
Предмет: Русский язык,
автор: Nastyshka205
Предмет: Математика,
автор: alinababicheva
Предмет: Русский язык,
автор: polinka456791