Предмет: Математика,
автор: raximovabonu1
Найдите радиус основания цилиндра наибольшего объема, который можно вписать в шар радиуса 6.
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
Рассмотрим осевое сечение. Пусть радиус окружности основания цилиндра равен тогда
Из теоремы Пифагора для прямоугольного треугольника
Объем цилиндра V = Sh = 2\pi {x^2}\sqrt {9 - {x^2}} .
Найдем производную где
— сложная функция:
Найдем максимум этой функции. Нули производной — числа и
С помощью метода интервалов видим, что функция возрастает от
до
и убывает после
таким образом
— точка ее максимума.
Приложения:

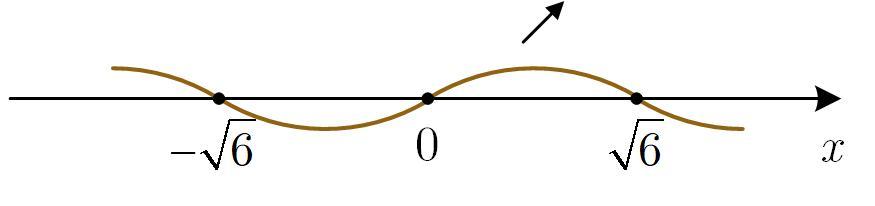
Похожие вопросы
Предмет: Английский язык,
автор: fatima25it
Предмет: Русский язык,
автор: EmmaKit69
Предмет: Українська мова,
автор: мексіке
Предмет: Алгебра,
автор: RaZgOn12
Предмет: Українська мова,
автор: alinahhh74