Question

Найти наибольший возможный объём цилиндра, площадь полной поверхности которого равна 24л.​

Answer 1

Ответ:

Наибольший возможный объем цилиндра равен $16\pi$

Пошаговое объяснение:

Пусть радиус основания цилиндра равен $r,$ а высота — $h.$ Тогда площадь боковой поверхности равна $2\pi rh,$ а сумма площадей верхнего и нижнего оснований — $2\pi {r^2}.$

По условию задачи

$2\pi rh + 2\pi {r^2} = 24\pi,$

откуда удобно выразить высоту:

$h = \displaystyle\frac{{24\pi - 2\pi {r^2}}}{{2\pi r}} = \displaystyle\frac{{12 - {r^2}}}{{r}}.$

Объем цилиндра

$V = \pi {r^2}h = \pi {r^2} \cdot \displaystyle\frac{{12 - {r^2}}}{{r}} = \pi r(12 - {r^2}) = 12\pi r - \pi {r^3}.$

Исследуем функцию $V(r),$ найдем ее производную:

$V'(r) = 12\pi - 3\pi {r^2}.$

Уравнение $V'(r) = 0$ дает корни $r = \pm 2.$

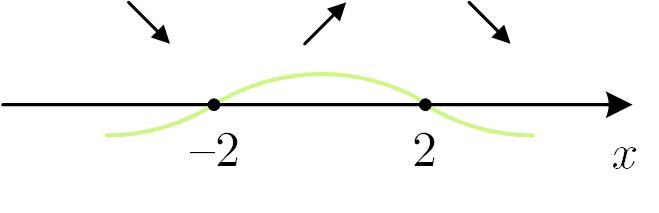
С помощью метода интервалов убеждаемся, что $r = 2$ является максимумом этой функции.

Тогда значение объема, соответствующего этому радиусу, равно

$V(2) = 12\pi\cdot2-\pi\cdot8=16\pi.$