Математика. Нужна помощь.
Даны вершины А(5; 3), В(-11; -9), С(-4; 15) треугольника АВС. Требуется найти:
а) уравнение стороны АС;
б) длину высоты, проведенной из вершины А;
в) величину угла В (в радианах).
Ответы
Даны вершины А(5; 3), В(-11; -9), С(-4; 15) треугольника АВС. Требуется найти:
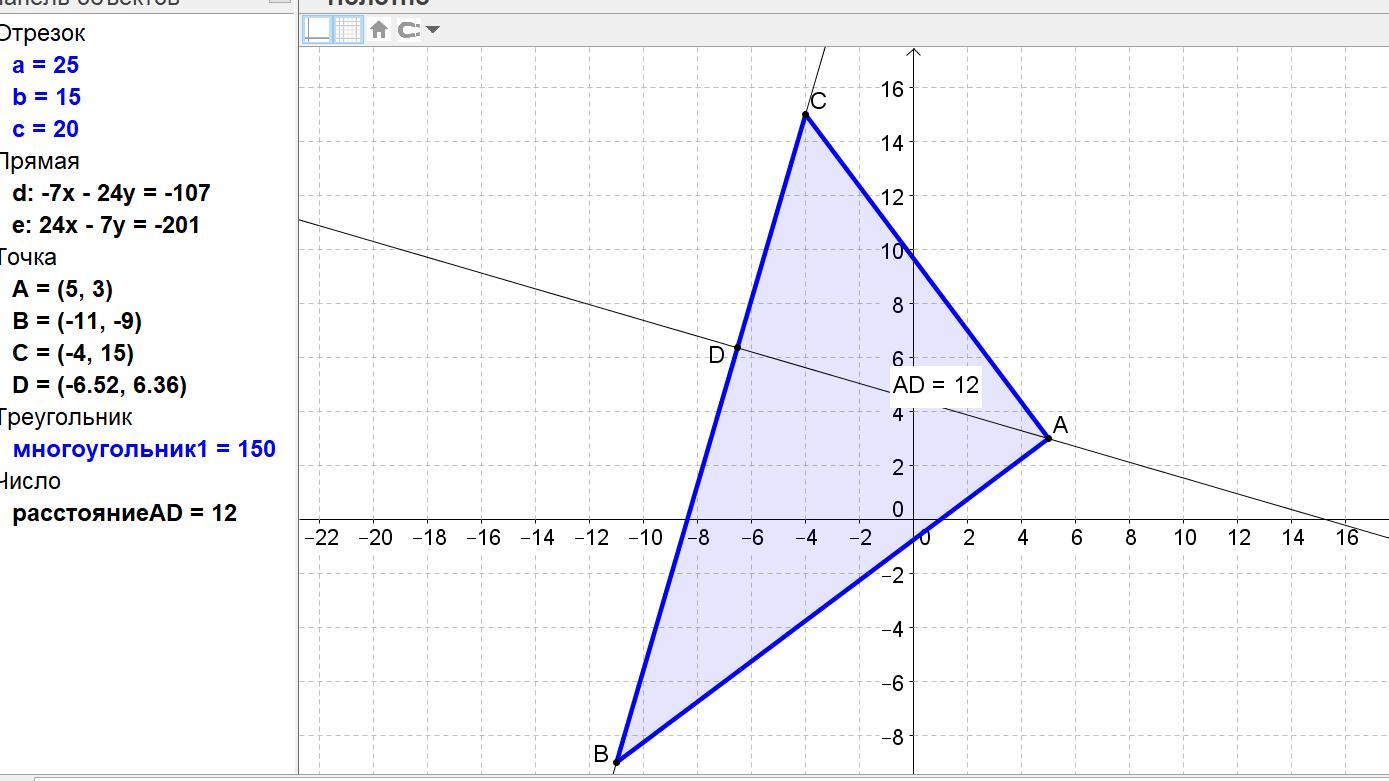
а) уравнение стороны АС: А(5; 3), С(-4; 15).
Вектор АС = (-4-5; 15-3) = (-9; 12).
уравнение стороны АС: (x – 5)/(-9) = (y – 3)/12 каноническое.
12*(x – 5) - (-9)*(y – 3) = 0,
12х – 60 + 9у – 27 = 0,
12х + 9у – 87 = 0, сократим на 3:
4х + 3у – 29 = 0 общего вида.
Выразим относительно у:
у = (-4/3)х + (29/3) с угловым коэффициентом.
б) длину высоты, проведенной из вершины А.
У прямой, перпендикулярной к прямой общего вида Ах + Ву + С = 0, коэффициенты А и В меняются на В и (-А) или (-В) и А.
Высота, проведенная из вершины А, - это перпендикуляр AD к стороне ВС.
Находим уравнение стороны ВС.
Вектор ВС = (-4-(-11); 15-(-9) = (7; 24).
Уравнение ВС: (x + 11)/7 = (y + 9)/24 каноническое.
24х + 264 – 7у – 63 = 0,
24х – 7у + 201 = 0 общего вида.
Для ВС общего вида 24х - 7у + 201 = 0 уравнение перпендикуляра АD будет таким – АD: 7х + 24у + С = 0.
Подставим координаты точки А(5; 3).
7*5 + 24*3 + С = 0, отсюда С = – 35 – 72 = -107.
Тогда получаем уравнение перпендикуляра AD к стороне BС в общем виде:
AD: 7х + 24у - 107 = 0 общего вида или у = (-7/24)х + (107/24) с угловым коэффициентом.
Находим точку D пересечения перпендикуляра со стороной ВС.
BC: 24х – 7у + 201 = 0 |x24 = 576x - 168y + 4824 = 0
AD: 7х + 24у - 107 = 0 |x7 = 49x + 168y – 749 = 0
625x + 4075 = 0,
x = -4075/625 = -6,52.
y = (24/7)*(-6,52) + (201/7) = -22,3543 +28,7143= 6,36.
D(-6,52; 6,36).
Отрезок AD = √((-6,52-5)² + (6,36-3)²) = √(132,7104 + 11,2896) = √144 = 12.
Можно применить второй вариант определения расстояния от точки А до прямой ВС.
Для вычисления расстояния от точки M(Mx; My) до прямой Ax + By + C = 0 используем формулу:
d = |A·Mx + B·My + C|/√(A² + B²)
Подставим в формулу данные:
d = |24·5 + (-7)·3 + 201|/√(24² + (-7)²) = |120 - 21 + 201|/√(576 + 49) =
= 300/√625 = 12.
в) величину угла В (в радианах).
Находим векторы ВА и ВС.
ВА = (5-(-11); 3-(-9)) = (16; 12),
модуль равен √(16²+ 12²) = √(256 + 144) = √400 = 20.
ВС = (-4-(-11); 15-(-9)) = (7; 24),
модуль равен √(7²+ 24²) = √(49+ 576) = √625 = 25.
Теперь находим косинус угла В:
cos B = (16*7+12*24)/(20*25) = 400/500 = 0,8.
Отсюда угол В = arccos 0,8 = 0,643501 радиан или 57,17432 градуса.