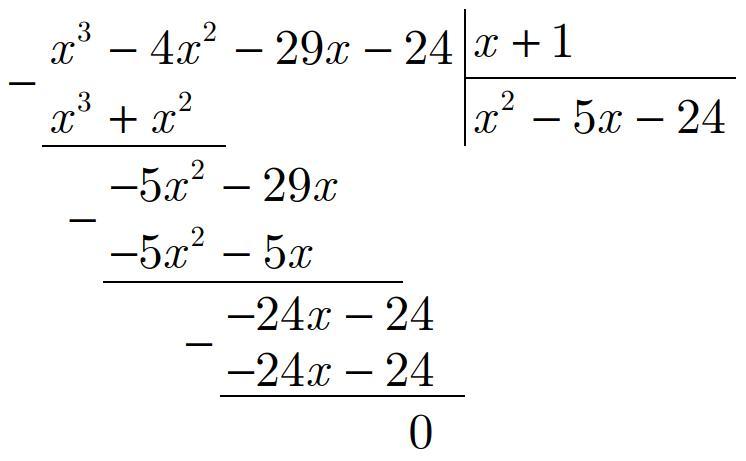Question

Разложи на множители многочлен

Answer 1

Ответ:

$(x + 1)(x + 3)(x - 8)$

Объяснение:

Обозначим $A(x)=x^3-4x^2-29x-24.$

Для разложения многочлена на множители найдем его корни (напомним, что корнями многочлена называются числа, которые превращают его в $0$).

Тогда если числа $x_1,$ $x_2,$ $x_3$ являются его корнями, то

$A(x)=(x-x_1)(x-x_2)(x-x_3).$

Согласно следствию из теоремы Безу целые корни такого многочлена следует искать среди делителей свободного члена. Делителями числа $-24$ являются числа  

$\pm 1,$  $\pm 2,$  $\pm 3,$  $\pm 4,$  $\pm 6,$  $\pm 8,$  $\pm 12,$  $\pm 24.$

Последовательно начиная подставлять их в указанной последовательности, убеждаемся, что одним из корней данного многочлена является число $-1.$

Это означает, что можно выделить линейный множитель, записав $A(x) = (x + 1)P(x).$

Для нахождения $P(x)$ выполним деление ${x^3} - 4{x^2} - 29x - 24$ на $x + 1$ в столбик (см. рисунок).

Получаем в частном квадратный трехчлен $P(x) = {x^2} - 5x - 24,$ корни которого легко найти с помощью теоремы Виета:

$\left\{ \begin{array}{l}{x_1} + {x_2} = 5,\\{x_1}{x_2} = - 24\end{array} \right.$

Перебором убеждаемся, что подходящие числа $-3$ и $8.$

Если числа $x_1$ и $x_2$ являются корнями квадратного трехчлена $ax^2+bx+c,$ то он раскладывается на множители:

$ax^2+bx+c=a(x-x_1)(x-x_2).$

Тогда ${x^2} - 5x - 24 = (x + 3)(x - 8),$ а исходный многочлен раскладывается на множители следующим способом: $A(x)={x^3} - 4{x^2} - 29x - 24=(x+1)P(x)= (x + 1)(x + 3)(x - 8).$