Question

допоможіть будь ласка ​

Answer 1

Большая диагональ ромба 12√3 см, а один из его углов 120°. Найти сторону и меньшую диагональ.

=========================

=========================

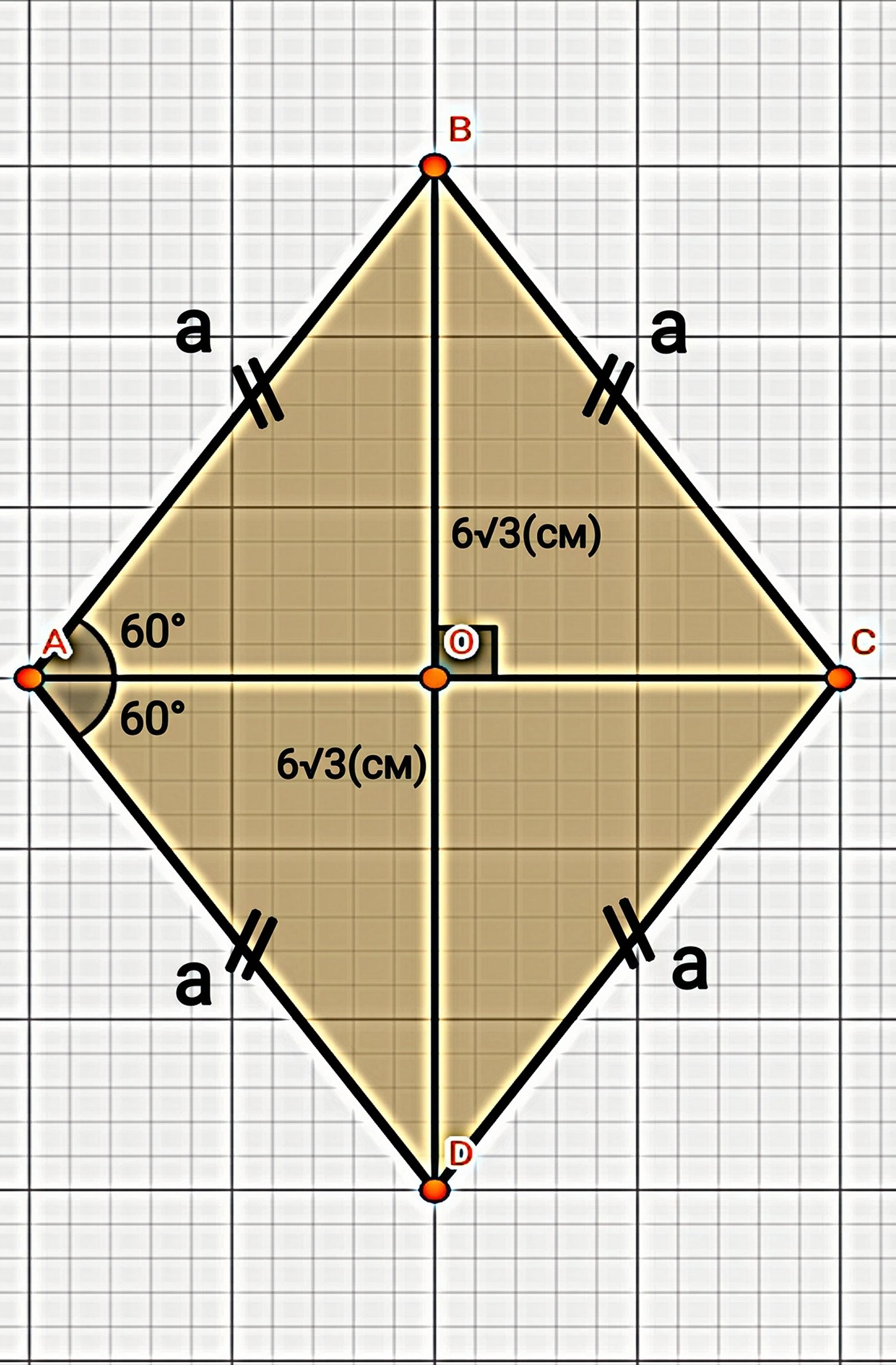
Дано: ABCD - ромб, BD = 12√3(см), ∠A = 120°

Найти: сторону, d₂ - ?

⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение

• Диагонали ромба перпендикулярны и точкой пересечения делятся попалам. ВО=DO=6√3см
• Диагонали ромба также являются биссектрисой углов ромба. ∠А=120°. Биссектриса (АС) разбивает ∠А на 60°.
• У ромба противоположные углы равны. ∠ВАС=∠ВСА=60°
• Рассмотрим ∆АВС. Найдем ∠В зная, что сумма углов любого треугольника равна 180°. Тогда ∠В= 180° - 60° - 60°= 60°. Отсюда выходит, что ∆АВС - равносторонний( по свойству равност./т).
• Биссектриса ВО также является высотой(по свойству равност./т).
• Из формулы высоты найдем сторону(а) ромба.

⠀⠀⠀Формула: $\large h= \frac{a\sqrt{3}}{2}$

⠀⠀⠀6√3=$\large \frac{a\sqrt{3}}{2}$

⠀⠀⠀6√3 * 2 = а√3

⠀⠀⠀а=12(см)

• Ромб - это параллелограмм, у которого все стороны равны. Следовательно все стороны ромба равны 12(см).
• Т.к. наш треугольник равносторонний, то все его стороны равны(по свойству р/т). Меньшая диагональ АС=12(см).

Проверка. ОС половина диагонали АС. Найдем катет ОС по теореме Пифагора и домножем на 2.

• Она гласит, что квадрат гипотенузы равен сумме квадратов катетов.

⠀⠀⠀ВС²=ВО²+ОС²

⠀⠀⠀12²=(6√3)²+ОС²

⠀⠀⠀144=108+ОС²

• Отсюда выразим катет ОС

⠀⠀⠀ОС²=144-108

⠀⠀⠀ОС²=36

• Извлечем корень.

⠀⠀⠀ОС= √36

⠀⠀⠀ОС=6(см)

⠀⠀⠀АС=6*2=12(см)

Ответ:Сторона и меньшая диагональ ромба равны 12(см)

Answer 2

Ответ:

12 см;  12 см.

Объяснение:

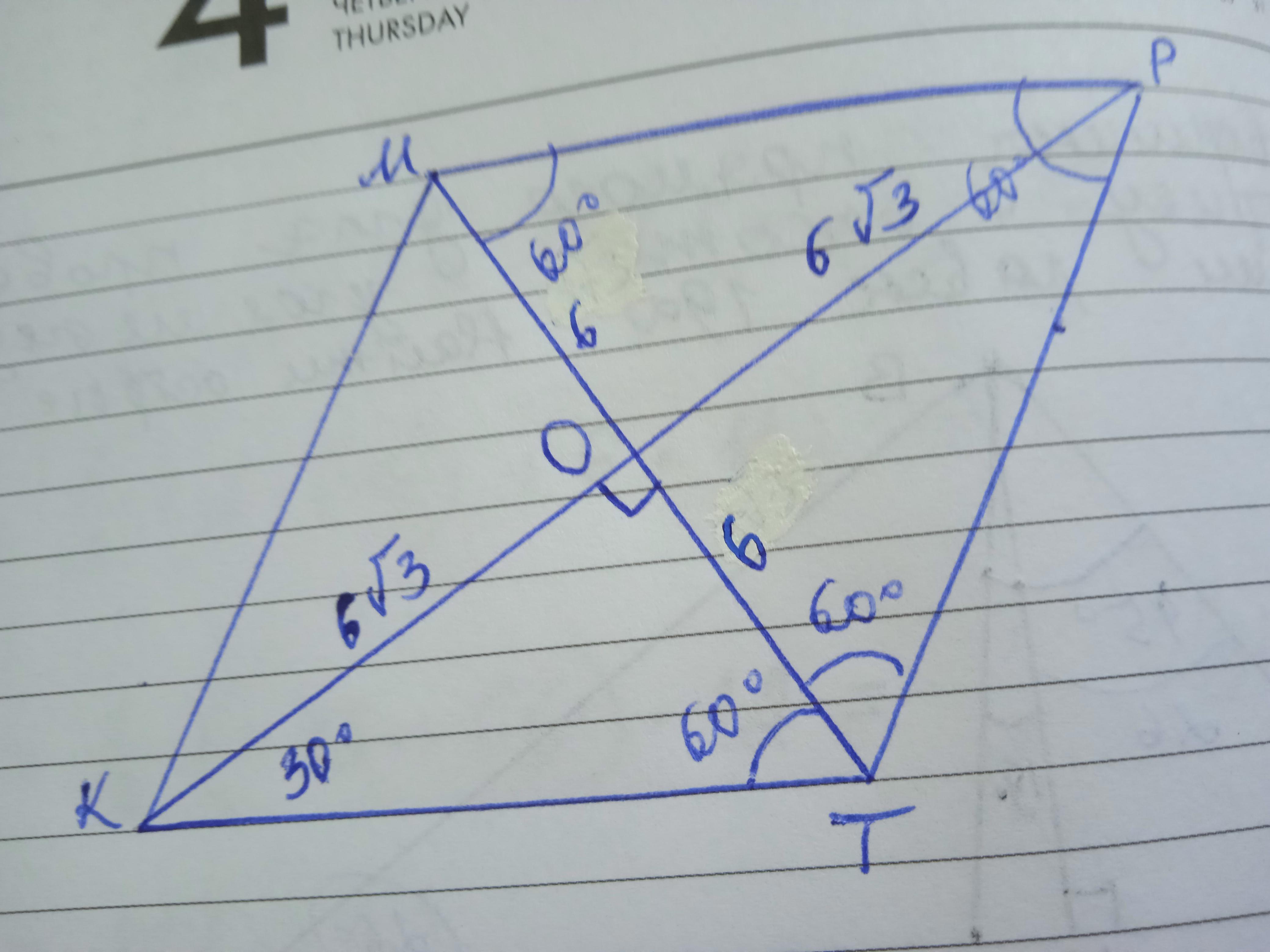
Дано: КМРТ - ромб,  ∠КТР=120°,  КР=12√3 см.  МТ - ?  КТ - ?

Всі сторони ромба рівні. Протилежні кути ромба рівні. Діагоналі ромба перетинаються під прямим кутом і в точці перетину діляться навпіл. Діагоналі ділять навпіл кути ромба. Діагоналі ділять ромб на чотири рівних прямокутних трикутника.

Отже КО=РО=12√3 : 2 = 6√3 см.

∠КТО=∠РТО=120:2=60°

ΔКОТ - прямокутний, ∠ТОК=90-60=30°

За теоремою синусів ТО=1/2 * 6√3 : √3/2 = 6 см.

МТ=2 ТО=12 см.

За теоремою Піфагора КТ²=КО²+ТО²=108+36=144;  КТ=12 см.