Предмет: Математика,
автор: gamesmonster
Найти производные y' =dy/dx заданных функций
Приложения:
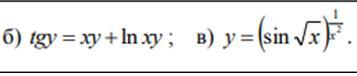
Ответы
Автор ответа:
1
Пошаговое объяснение:
б)
Подразумеваем, что дифференцируем обе части по
Так, — сложная функция, поэтому ее производная это сперва производная от тангенса, умноженная на производную от его аргумента
:
Находим производную xy как производную произведения:
Производная логарифма — опять сложная функция:
Вместе получаем:
Выражаем из последнего равенства. Можно преобразовать ответ, избавившись от «двухэтажных» дробей:
в)
Прологарифмируем по натуральному основанию обе части данного равенства: Теперь найдем производную от обеих частей аналогично решению п. б).
Похожие вопросы
Предмет: Английский язык,
автор: daniiltum
Предмет: Английский язык,
автор: KartesFus
Предмет: Русский язык,
автор: nastyashvarts
Предмет: Математика,
автор: armanovi05
Предмет: Алгебра,
автор: sofyakolupaeva02