Предмет: Геометрия,
автор: 27sashashevchenko
У трикутнику ABC <A - тупий, ВС = 20 см, AB = 15 см, ВК = 12 см висота трикутника. Знайдіть АС. -
Ответы
Автор ответа:
0
Ответ:
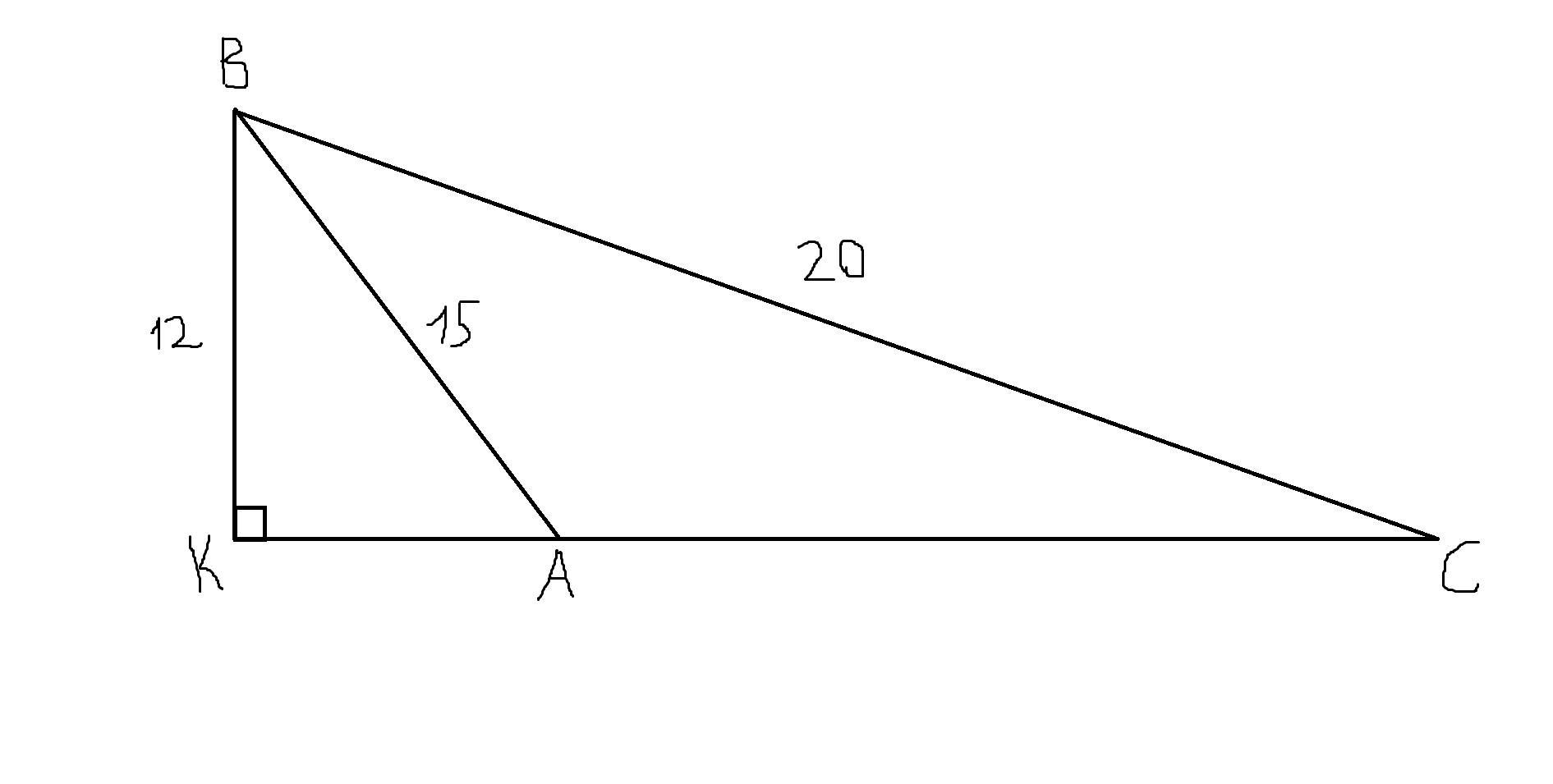
Розглянемо ΔКВС - він прямокутний (∠ВКС=90°), тоді:
за теоремою Піфагора КС=√(ВС²-ВК²)
КС=√(20²-12²)=√(400-144)=√256=16 (см)
Розглянемо ΔКВА- він прямокутний (∠ВКА=90°), тоді:
за теоремою Піфагора КА=√(АВ²-ВК²)
КА=√(15²-12²)=√(225-144)=√81=9 (см)
АС=КС-КА=16-9=7 (см)
Відповідь: АС=7 см
Приложения:
Автор ответа:
1
***
дано:
ΔАВС
∠А - тупой
ВС = 20 см
AB = 15 см
ВК = 12 см - высота
решение:
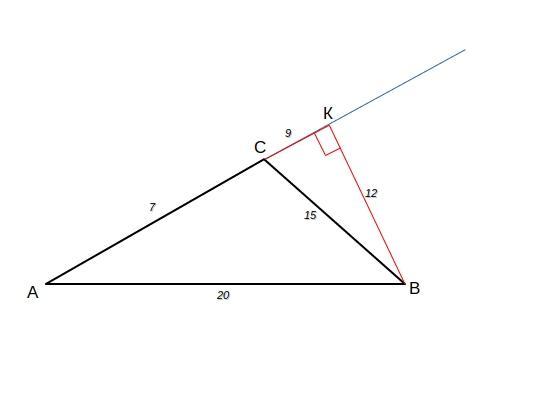
из треугольника АВС угол С тупой,
значит высота ВК опустится на продолжение стороны АС
следовательно ВК⊥АК
из прям. треугольника АКВ по Пифагору:
АК² = АВ² - ВК²
АК = √(АВ² - ВК²)
АК = √(20² - 12²) = 16 см
из прям. треугольника СКВ по Пифагору:
СК² = ВС² - ВК²
СК = √(ВС² - ВК²)
СК = √(15² - 12²) = 9 см
⇔
АС = АК - СК = 16 - 9 = 7см
ответ: АС = 7см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Milanka2006
Предмет: Окружающий мир,
автор: Аноним
Предмет: Английский язык,
автор: odarchenkonadezhda
Предмет: Английский язык,
автор: asanet
Предмет: Французский язык,
автор: 79163627217