Предмет: Алгебра,
автор: enderkiril806
номер 4.2 помогите пожалуйста
Приложения:
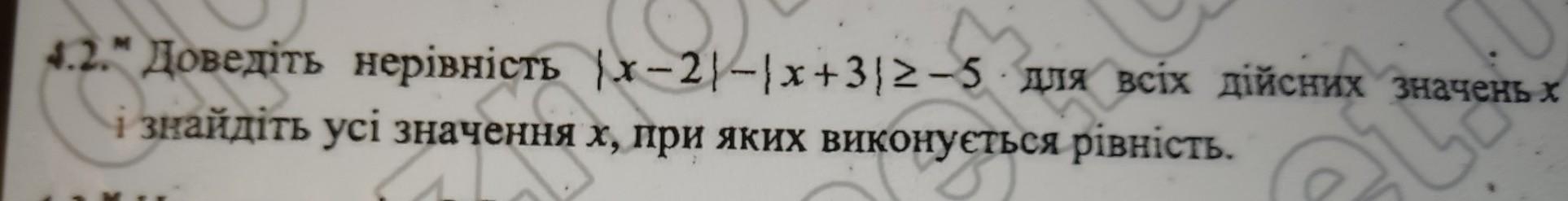
Ответы
Автор ответа:
2
Ответ:
Объяснение:
Полезные свойства модулей :
1) | a | + | b | ≥ | a + b |
2) | a | + | b | = | a + b | ⇔ a · b ≥ 0
Ваше неравенство можно записать так : | x - 2 | + | 5 | ≥ | x +3 | ( 1 )
пусть a = x - 2 ; b = 5 , тогда неравенство примет вид :
| a | + | b | ≥ | a + b | и так как оно справедливо дя всех a и b ,
то неравенство ( 1 ) справедливо для всех х
| a | + | b | = | a + b | ⇔ a · b ≥ 0 ⇔ ( x - 2) · 5 ≥ 0 ⇔ x ≥ 2
значит равенство имеет место для всех x ≥ 2
antonovm:
решение короткое ( без раскрытия модулей ) , но правильность гарантирую
Идеально, как всегда
Спасибо , Тамара
Автор ответа:
1
Відповідь: розв'язання завдання додаю
Пояснення:
Приложения:

Похожие вопросы
Предмет: Окружающий мир,
автор: Арайка2222
Предмет: Русский язык,
автор: Pari7777
Предмет: Русский язык,
автор: Алена041
Предмет: Геометрия,
автор: DianaSerpiente
Предмет: Математика,
автор: gulnazalatypova