Предмет: Алгебра,
автор: dmitrybborisov
Разложи на множители многочлен
Приложения:

Ответы
Автор ответа:
2
Ответ:
Объяснение:
По теореме Безу если такой многочлен имеет целые корни, их надо искать среди делителей числа 10: Легко убедиться, что
обращает левую часть в 0. Пользуясь схемой Горнера или деля исходный многочлен на
в столбик, получаем:
Вторая скобка представляет из себя квадратный трехчлен. По теореме Виета
можно подобрать его корни
Тогда, учитывая, что
получаем, что
а значит и
Приложения:
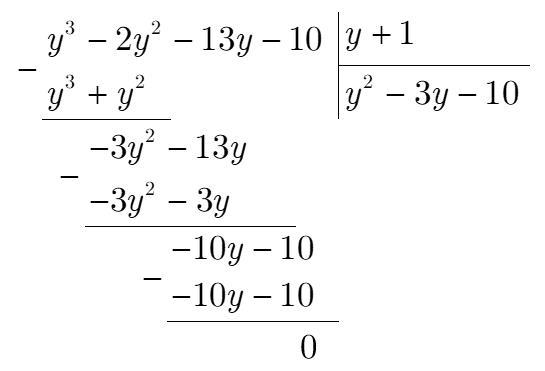
Похожие вопросы
Предмет: Окружающий мир,
автор: 229dogis
Предмет: Русский язык,
автор: геля159
Предмет: Русский язык,
автор: vasilisa64
Предмет: Геометрия,
автор: chelovek6679
Предмет: Алгебра,
автор: marina34557