Найдите высоту правильной треугольной пирамиды, если площадь боковой грани равна 20√3, а окружность, вписанная в основание имеет радиус 4.
Ответы
Ответ:
Высота правильной треугольной пирамиды равна 3 (единицы измерения)
Пошаговое объяснение:
Найдите высоту правильной треугольной пирамиды, если площадь боковой грани равна 20√3, а окружность, вписанная в основание имеет радиус 4.
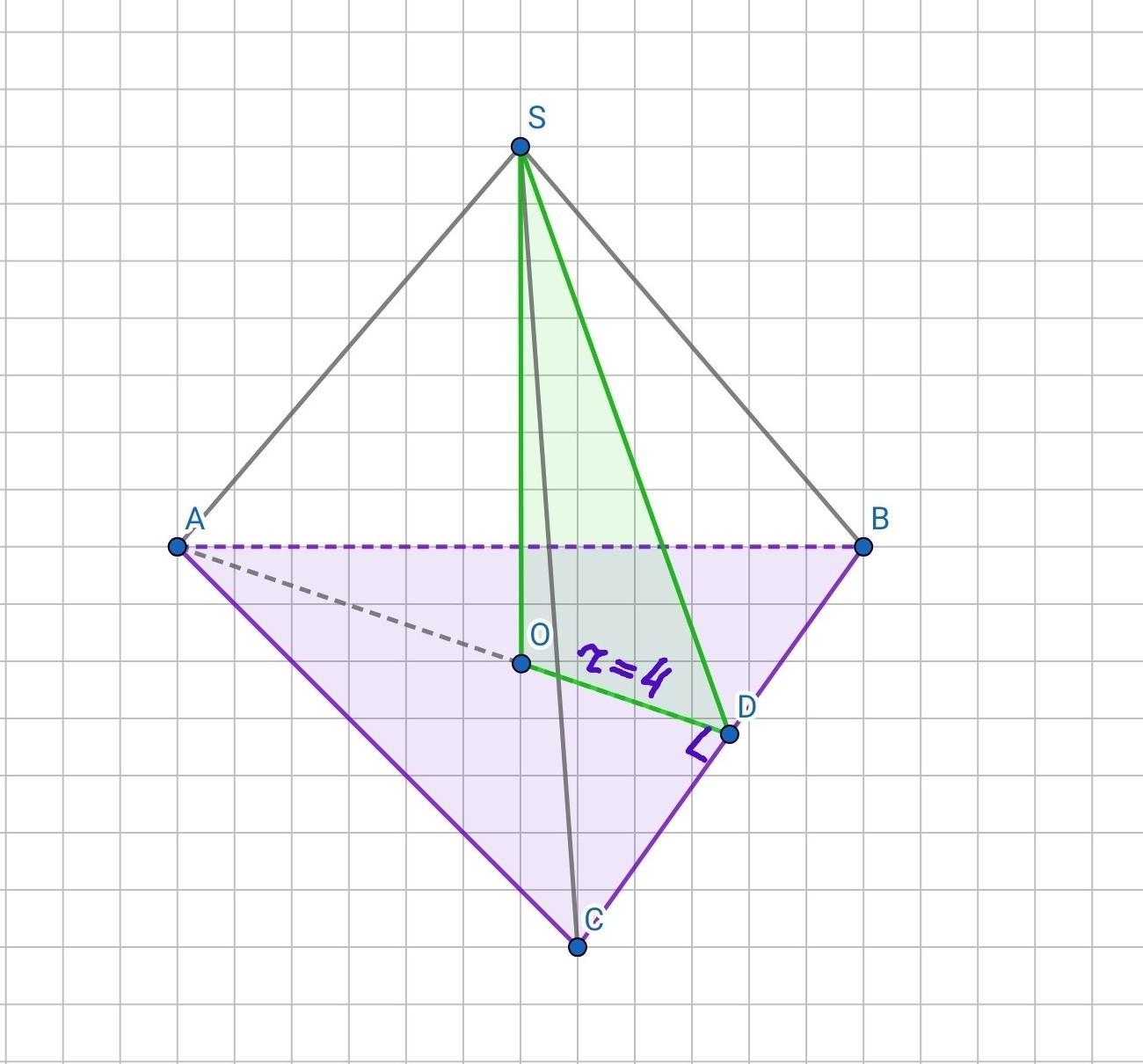
В основании правильной треугольной пирамиды SABC лежит правильный (равносторонний) △ ABC.
Высота SO правильной треугольной пирамиды проектируется в центр вписанной в △ABC и описанной около △ABC окружности ( в равностороннем треугольнике они совпадают).
r=OD=4 ед- по условию.
Радиус вписанной окружности в равностороннем треугольнике:
где a - сторона △ABC.
а = BC = r • 2√3 = 4 • 2√3 = 8√3 ед
Площадь боковой грани (площадь треугольника) вычисляется по формуле:
где SD - высота боковой грани (апофема пирамиды). SD⟂BC.
S=20√3 - по условию. Следовательно:
½ • 8√3 • SD = 20√3
SD = 20 : 4 = 5 ед
Поскольку высота SO перпендикулярна к площади основания (△ABC), то она перпендикулярна к любой прямой, принадлежащей основанию. => SO⟂OD.
В прямоугольном треугольнике SOD(∠O=90°) по теореме Пифагора найдём катет SO:
SO² = SD²-OD² = 5²-4² = 25-16 = 9
SO = √9 = 3 ед
Высота правильной треугольной пирамиды равна 3 (ед)
#SPJ1