Предмет: Геометрия,
автор: anna063pink
Помогите пожалуйста!!!
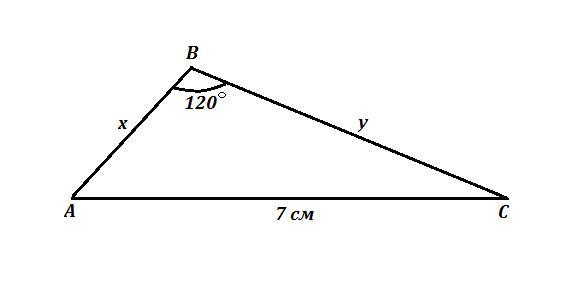
Одна из сторон треугольника равна 7 см, а две другие образуют угол 120°. Найти меньшую из неизвестных сторон треугольника, если его периметр равен 15 см.
Ответы
Автор ответа:
1
Решение.
ΔАВС , АС=7 см , ∠В=120° , Р=15 см .
Найти меньшую из неизвестных сторон .
Обозначит х=АВ , у=ВС .
По теореме косинусов имеем:
Так как периметр Р=х+у+7 , то х+у=Р-7 , х+у=15-7 , х+у=8 (см) .
По формуле квадрата суммы получим
Подставим в уравнение (*) выражение для х²+у² :
Теперь решим систему.
Корни уравнения нашли по теореме Виета .
Итак, нашли две неизвестные стороны треугольника АВ и ВС .
Либо АВ=3 см , ВС=5 см , либо АВ=5 см , ВС =3 см .
Ответ: меньшая из неизвестных сторон равна 3 см .
Приложения:
Автор ответа:
0
Ответ:
3 см.
Объяснение:
Приложения:

Похожие вопросы
Предмет: Английский язык,
автор: ира832
Предмет: Русский язык,
автор: tanyhkaalekseev
Предмет: Русский язык,
автор: ооо262
Предмет: Алгебра,
автор: richaarrrd
Предмет: Алгебра,
автор: ginhemp