Предмет: Математика,
автор: soleil03
СРОЧНО!
Дан треугольник ABC со стороной BC=2 и sin A=4/5.Чему равно AC-?
Приложения:
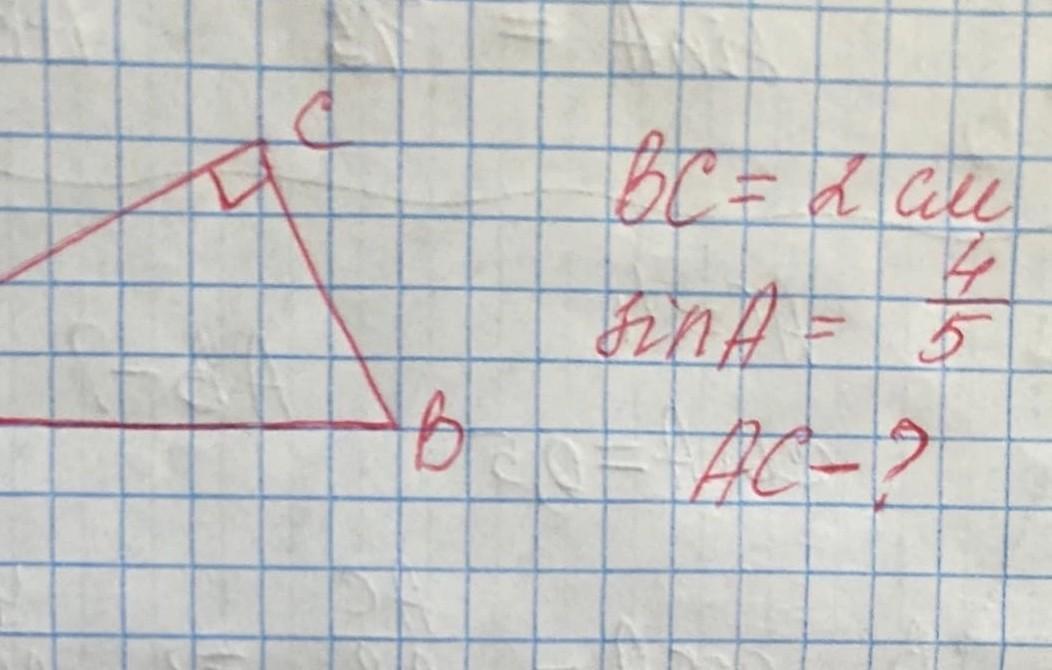
Ответы
Автор ответа:
0
Синусом угла прямоугольного треугольника называется отношение длины противолежащего этому углу катета к длине гипотенузы.
AC найдём по теореме Пифагора :
Автор ответа:
0
Ответ:
АС=1,5 см
Пошаговое объяснение:
sinA=BC/AB
AB=BC/sinA=2/(4/5)=2,5 см
по теореме Пифагора:
АС=√(АВ²-ВС²)=√(2,5²-2²)=√(6,25-4)=1,5 см
Похожие вопросы
Предмет: Русский язык,
автор: marinasmiIe167
Предмет: Қазақ тiлi,
автор: asmagieva
Предмет: Русский язык,
автор: Nikita334555
Предмет: Физика,
автор: helpmepls957