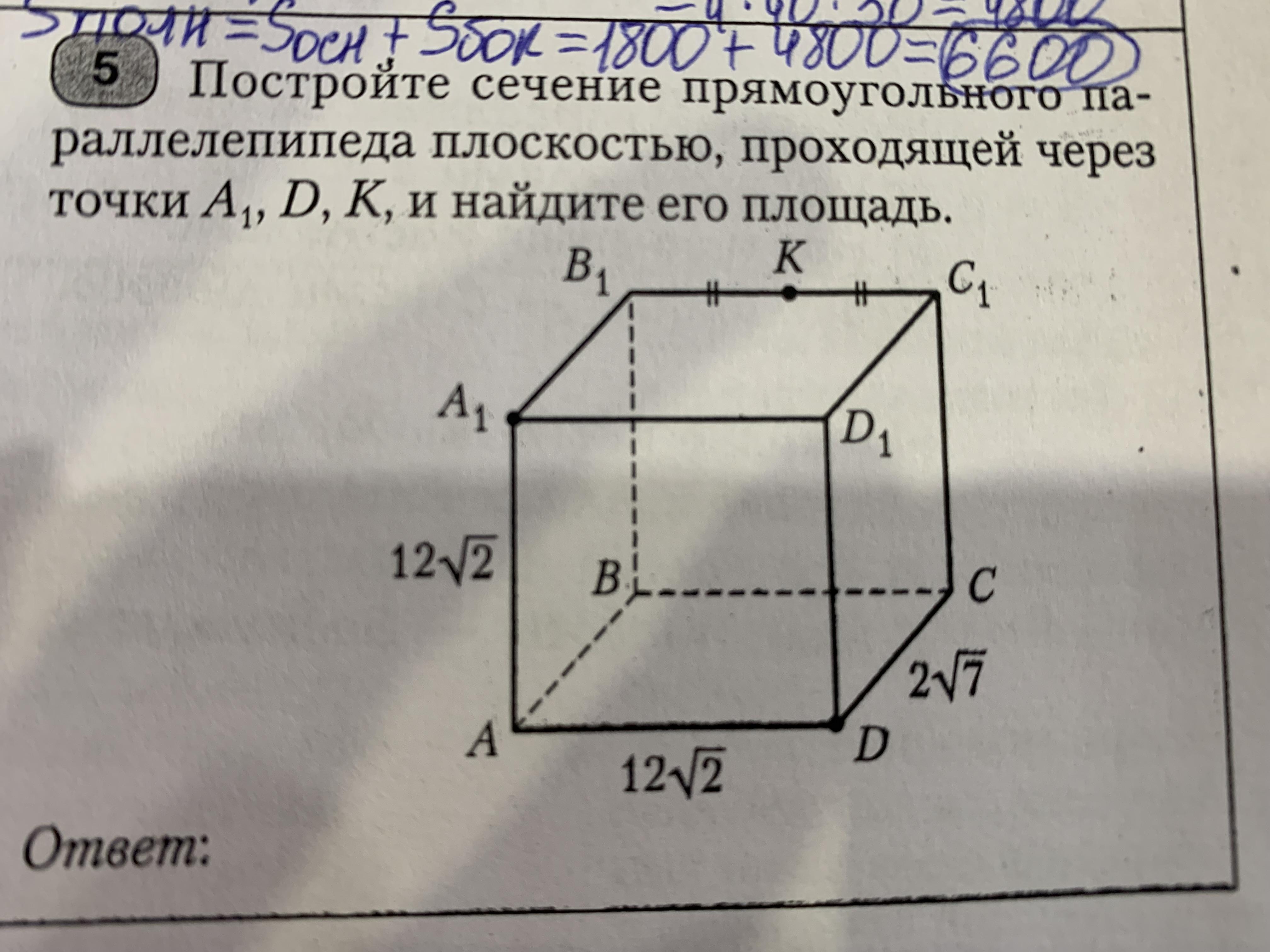
Постройте сечение прямоугольного параллелепипеда плоскостью, проходящей через точки А1, Д, К, и найдите его площадь
Ответы
Ответ:
желтый -дополнительные построения, красный - ключевые точки, зеленый - сечение
пусть дополнительная точка будет Е.
в сечении трапеция с основаниями ке и а1д
s=(ке+а1д)×h/2
точка е будет серединой отрезка с1с, тогда можем рассмотреть равнобедренный прямоугольный треугольник кс1е.
катеты равны между собой и равны половине грани параллелепипеда кс1=с1е=6 корень 2
по теореме пифагора гипотинуза ке=корень (кс1^2+с1е^2)=корень (36×2+36×2)=6×2=12
также с а1д
а1д=корень(а1а^2+ад^2)=12×2=24
высота h. заметим, что сечение это равнобедренная трапеция, а значит можем из большего основания вычесть меньшее и остаток разделить на 2, затем по теореме пифагора нацдем искомое.
24-12=12
12/2=6 (это отрезок а1м)
пусть высота это прямая км, где м точка лежпщая на прямой а1д.
рассмотрим теугольник а1мк, он прямоугольный.
найдем вторую сторону этого треугольника а1к из треугольника а1в1к
а1к=корень(а1в1^2+в1к^2)=корень((2 корень 7)^2+(6корень 2)^2)=корень (4×7+36×2)=корень(28+72)=корень(100)=10
км=корень(а1к^2-а1м^2)=корень(10^2-6^2)=корень(100-36)=корень 64=8
s=(12+24)×8/2=36×4=144
ответ 144
