Предмет: Геометрия,
автор: Аноним
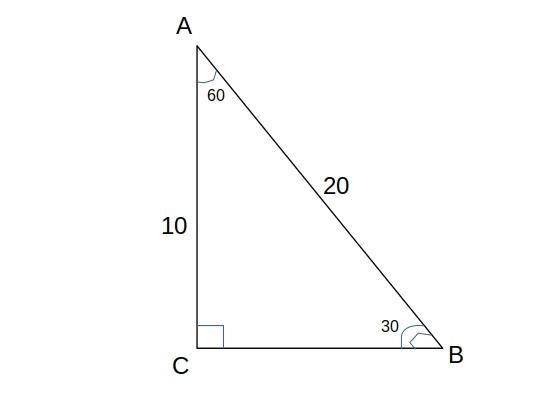
знайти катети прямокутного трикутника АВС (<С 90⁰) , якщо гипотенуза = 20 см , а <А =60⁰
Ответы
Автор ответа:
1
Ответ:
10 см; 10√3 см.
Объяснение:
∠В=90-60=30°, отже катет АС=1/2 АВ=20:2=10 см.
За теоремою Піфагора ВС=√(АВ²-АС²)=√(400-100)=√300=10√3 см.
Автор ответа:
2
***
дано:
прямоугольник АСВ
∠С = 90°
∠А = 60°
АВ = 20 см
----------------
найти АС и СВ
решение:
поскольку сумма острых углов прямоугольника равна 90°
неизвестный угол В равен 180° - 90° - 60° = 30°
т.к катет против угла 30° равна половине гипотенузы
⇔
АС = 1/2 АВ
АС = 20/2
АС = 10 см
теперь находим катет СВ по теореме Пифагора:
сумма квадратов длин катетов равна квадрату длины гипотенузы
c² = a² + b²
AB² = AC² + CB²
отсюда
CB² = AB² - AC²
CB² = (20)² - (10)²
CB² = 400 - 100 = 300
CB = √300 = √(3 · 100) = 10√3 см
ответ: катеты прямоугольного ΔАСВ равны 10√3 см и 10 см
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: sweta40
Предмет: Русский язык,
автор: lyuba39
Предмет: Қазақ тiлi,
автор: asemkartbaeva
Предмет: Физика,
автор: agentgirl51
Предмет: Математика,
автор: qwber