Предмет: Геометрия,
автор: Akvlt
В правильной треугольной пирамиде боковые ребра наклонены к плоскости основания под углом 45 градусов. Длина стороны основания равна  . Найдите расстояние между ребром основания и скрещивающимся с ним боковым ребром
. Найдите расстояние между ребром основания и скрещивающимся с ним боковым ребром
Ответы
Автор ответа:
1
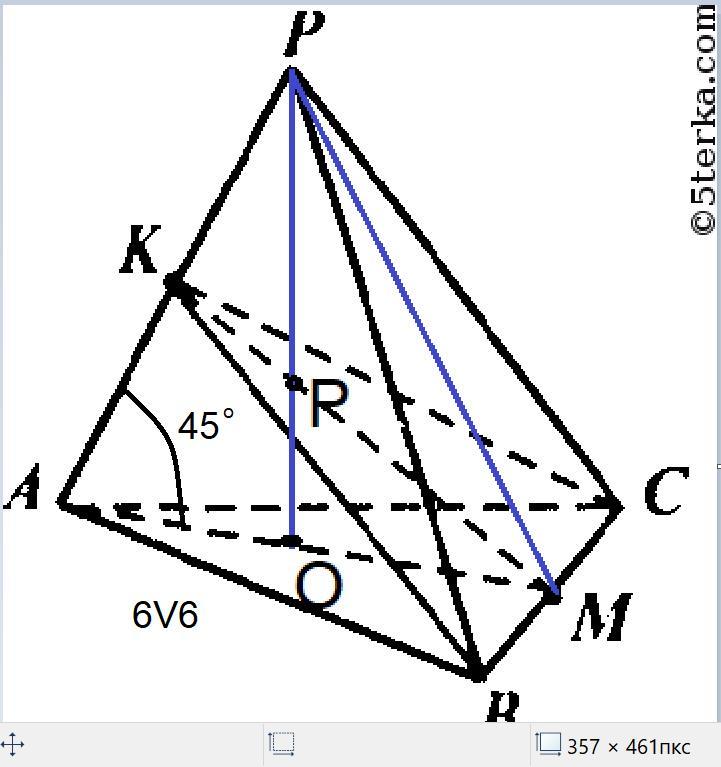
В правильной треугольной пирамиде боковые ребра наклонены к плоскости основания под углом 45 градусов. Длина стороны основания равна 6√6.
Надо найти расстояние между ребром основания и скрещивающимся с ним боковым ребром, то есть надо найти длину перпендикуляра МК из точки М (это середина стороны ВС основания) к ребру АР.
Из прямоугольного треугольника АКМ находим:
MK = AM*sin 45°.
АМ – это высота основания, она равна 6√6*cos 30° = 6√6*√3/2 = 9√2.
Тогда MK = 9√2*(√2/2) = 9.
Ответ: 9.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: dtd225
Предмет: Русский язык,
автор: kirika1
Предмет: Русский язык,
автор: nikta034
Предмет: Русский язык,
автор: miko77745