Предмет: Математика,
автор: babyshkalala
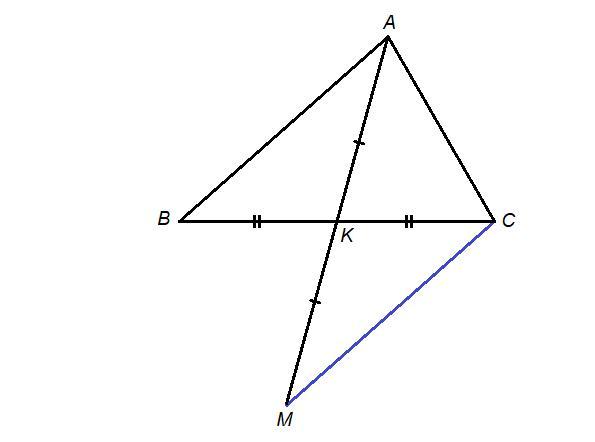
Медиана АК треугольника АВС продолжена за сторону ВС на отрезок КМ равный АК. Точка М соединяется с точкой С так что образуется треугольник МКС. Какому треугольнику он равен, исходя из 1 признака равенства треугольников?? с объяснением пжлст
Ответы
Автор ответа:
1
Ответ:
ΔMKC = ΔAKB
Пошаговое объяснение:
Первый признак равенства треугольников:
- если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
КМ = АК по условию,
ВК = СК, так как АК медиана (значит К - середина стороны ВС),
∠МКС = ∠АКВ как вертикальные, следовательно
ΔMKC = ΔAKB по первому признаку равенства треугольников (по двум сторонам и углу между ними).
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Мороженка24
Предмет: Русский язык,
автор: кадиря
Предмет: Русский язык,
автор: катрин861
Предмет: Окружающий мир,
автор: windabox128
Предмет: Геометрия,
автор: yacik550