Предмет: Алгебра,
автор: ivankakos61
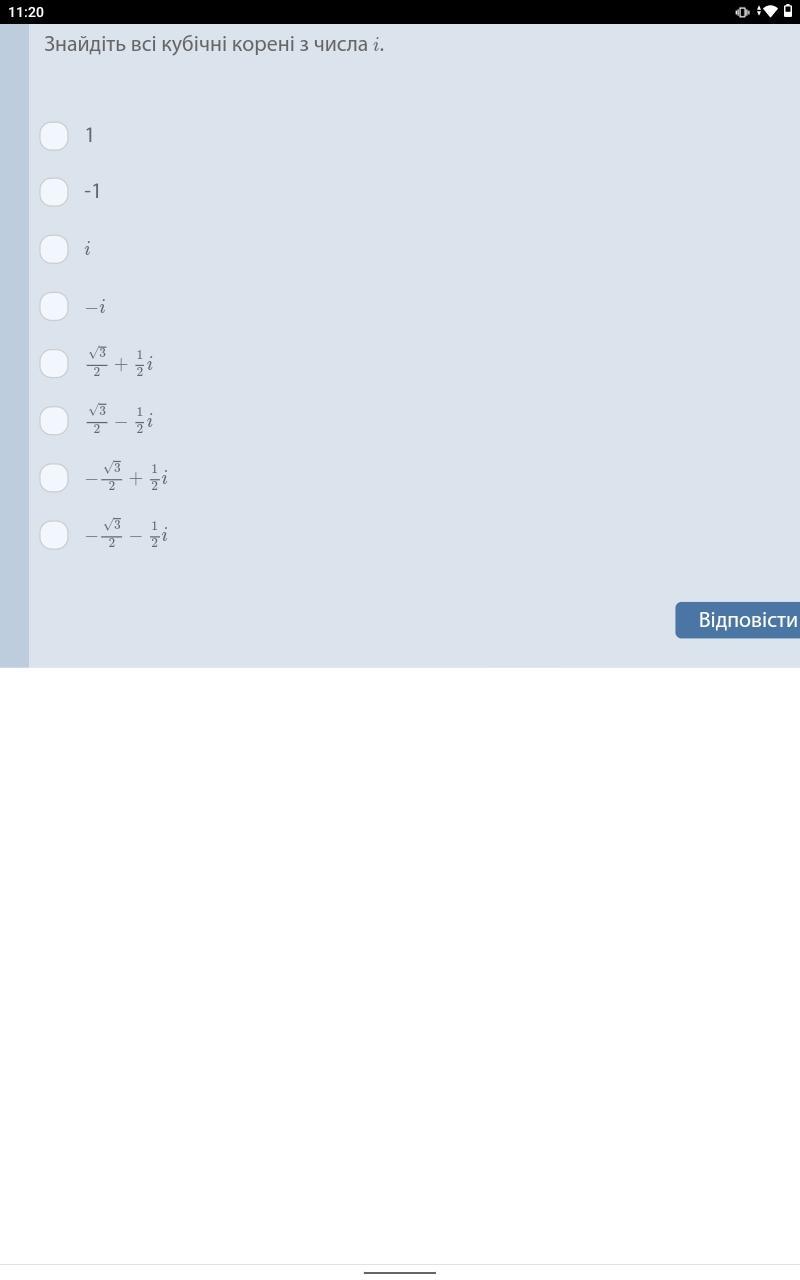
Помогите пожалуйста. Вопрос во вложении
Приложения:
BMW52:
3) 4) 5)
Нет
Ошибка.
Ответы
Автор ответа:
1
Решим уравнение .
Представим оба числа в тригонометрической форме:
Используем формулу Муавра:
Приравняем аргументы (учитывая периодичность):
Из этой формулы получим три корня, принадлежащих промежутку :
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: илья1552
Предмет: Английский язык,
автор: Аноним
Предмет: Другие предметы,
автор: weresowu
Предмет: Литература,
автор: pryhodzichdavid
Предмет: Химия,
автор: lelyavavilkina