Question

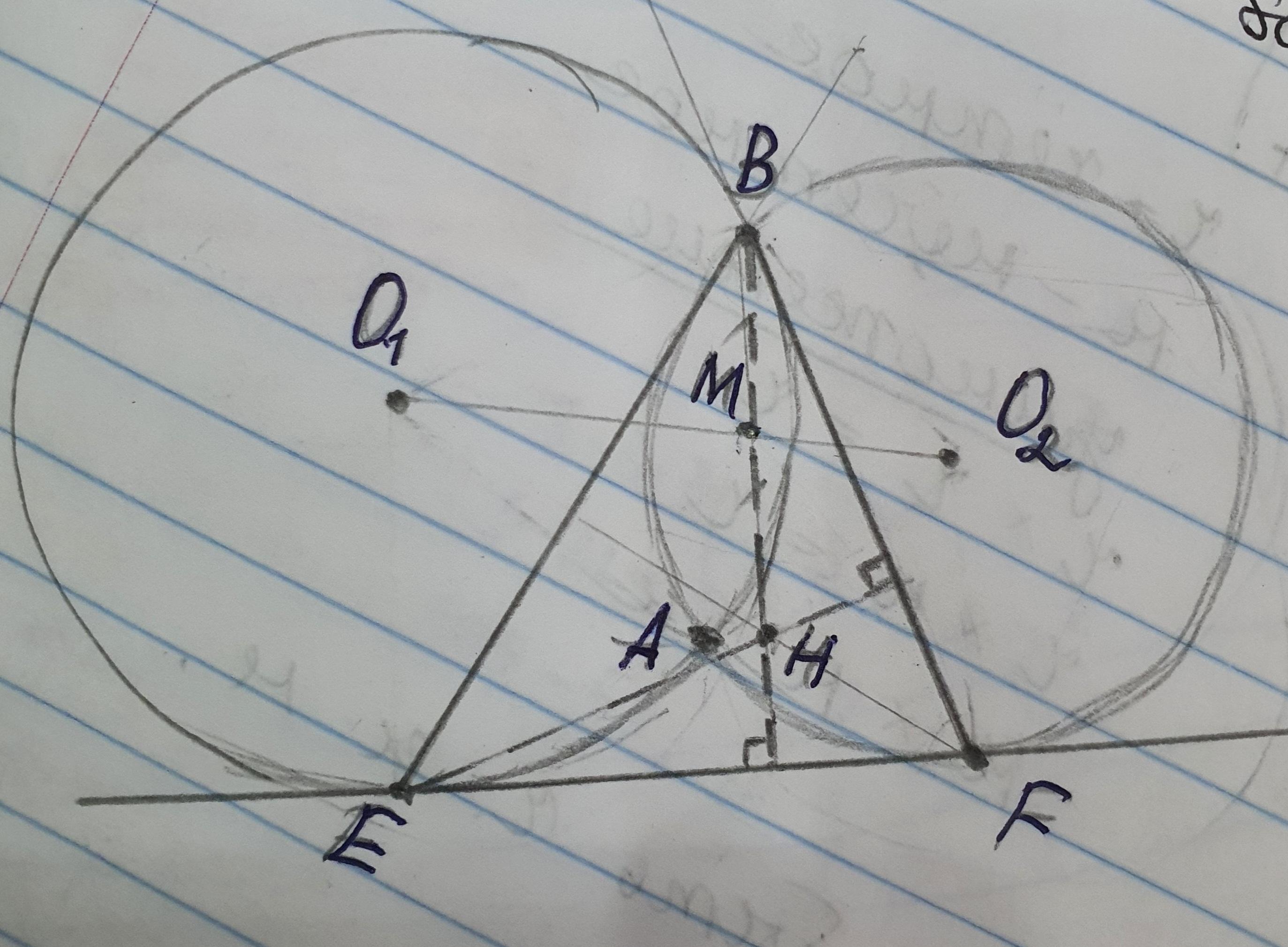
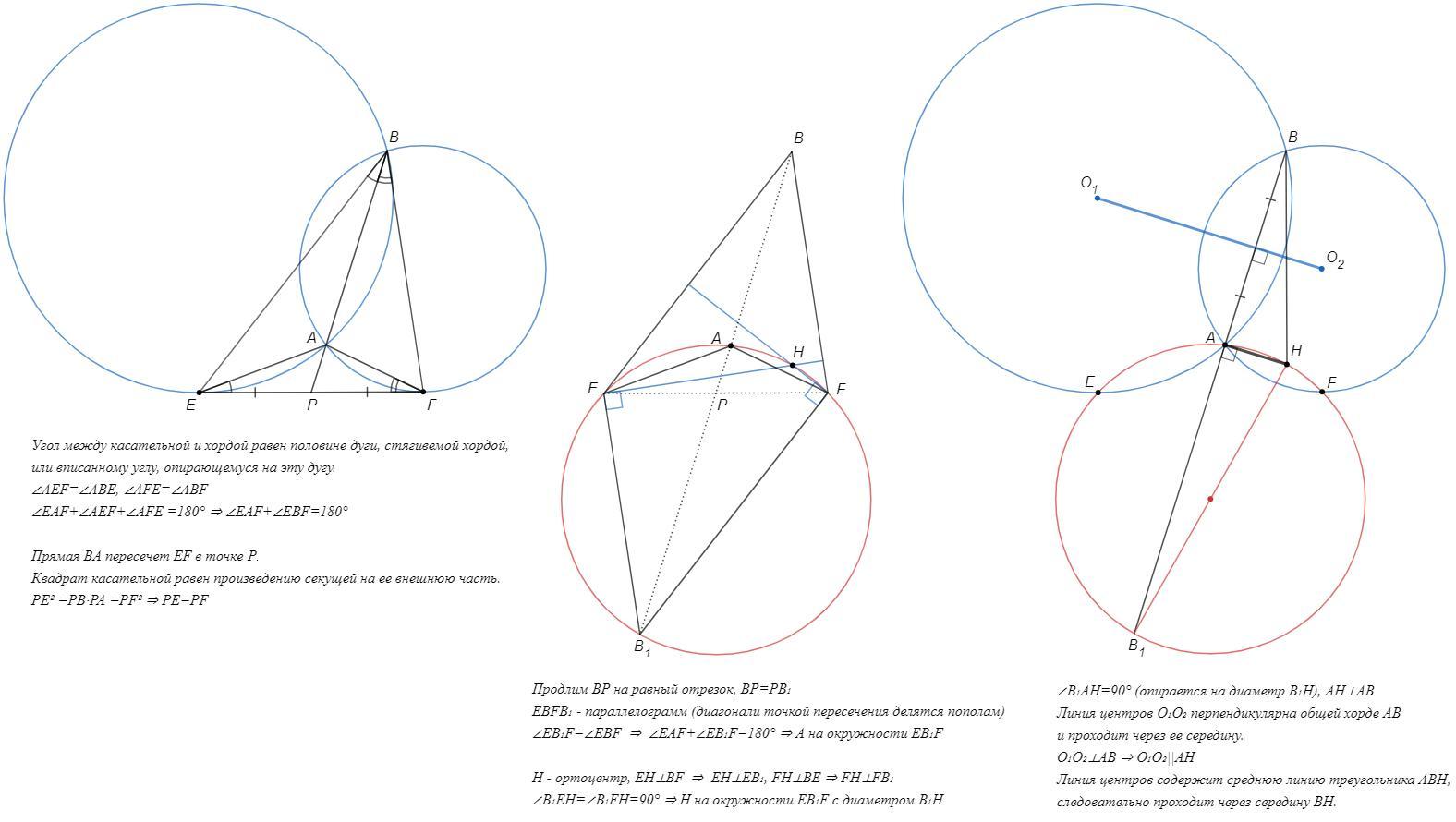
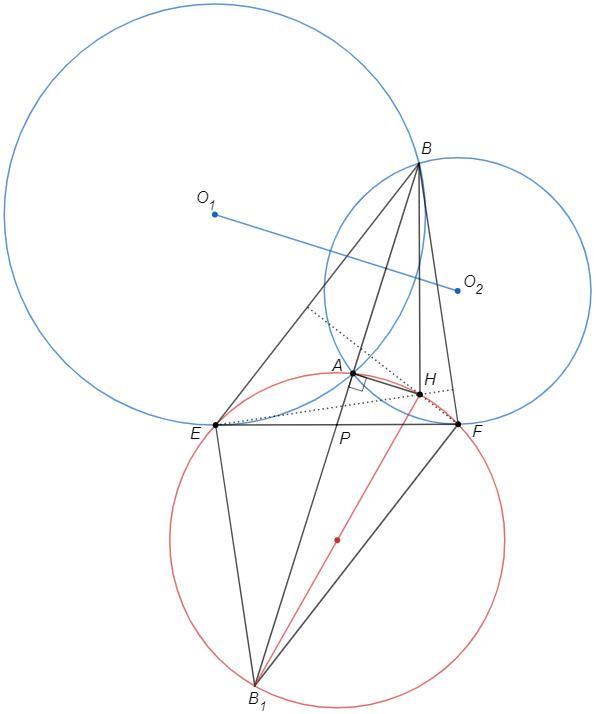
Две окружности пересекаются в точках A и B. Прямая касается двух окружностей в точках Е и F. Предположим, что A принадлежит внутренности треугольника BEF. Пусть H — ортоцентр треугольника BEF, а M — середина отрезка BH. Докажите, что M лежит на прямой, проходящей через центры двух окружностей.

Примечание. Ортоцентр треугольника — это точка пересечения его высот.

Answer 1

-----------------------------------------------------------------------