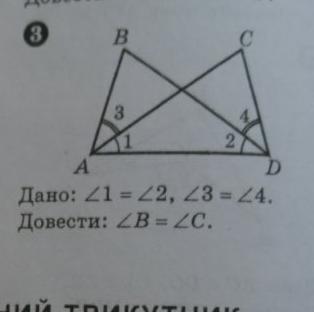
Дано: угл1 = угл2, угл3 = угл4.
Довести: углB=углC.
Ответы
(примечание: "<" - угол)
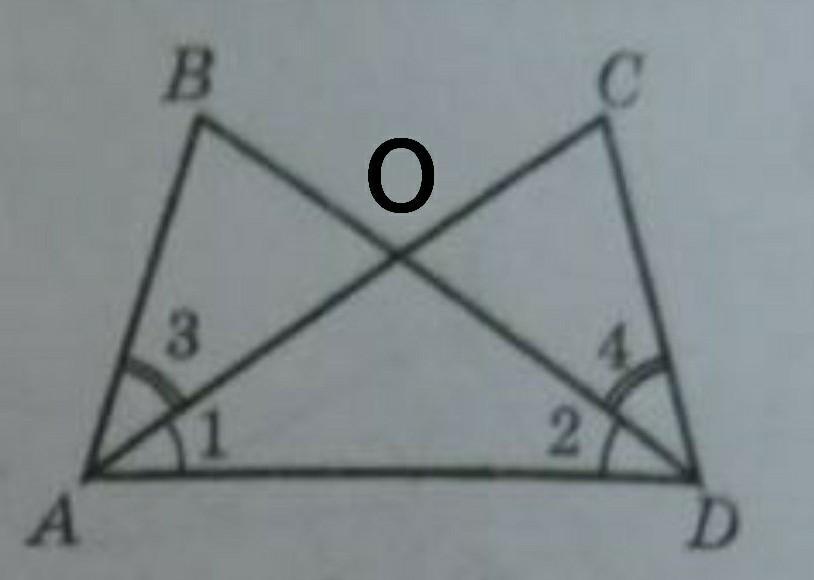
Рассмотрим треугольники BAO и СОD:
<BAO=<CDA=b (по условию)
<BOA=<COD=а (как вертикальные)
<B=180°-<ВАО-<ВОА=180°-b-a
<С=180°-<СDA-<COD=180°-b-a =>
<B=<C=180°-b-a
ч.т.д.
(зачем тут равенство первого и второго угла я не очень понимаю, но предполагаю, что составители хотят немного другой способ, так что его я тоже могу сделать)
Способ 2:
Рассмотрим треугольник АОD:
так как <1=<2, то треугольник АОD - равнобедренный, следовательно, АО=ОD
Рассмотрим треугольники BAO и СОD:
<BAO=<CDA (по условию)
<BOA=<COD (как вертикальные)
АО=ОD (так как АОD - равнобедренный)
Следовательно, треугольники ВАО и СОD равны по 2-ому признаку, а значит, <В=<С
ч.т.д.
Ответ:
Можно я все упрощу?
Из ΔABD и ΔDCA
∠B=180°-∠2-(∠1+∠3)=180°-∠1-∠2-∠3
∠C=180°-∠1-(∠2+∠4)=180°-∠1-∠2-∠4
Т.к. ∠3=∠4, то ∠B=∠C
Объяснение: