Предмет: Геометрия,
автор: Аноним
У трикутнику медіана дорівнює половині сторони, до якої вона проведена. Довести що один з кутів цього трикутника дорівнює сумі двох інших
cos20093:
Свою копейку в эту легонькую задачку. Вершина, из которой проведена медиана, лежит на окружности, построенной на стороне, как на диаметре (это просто условие, пересказанное другими словами). То есть угол напротив заданной стороны - вписанный и опирается на диаметр, то есть прямой. Дальше все очевидно.
Ответы
Автор ответа:
0
Объяснение:
Якщо медіана дорівнює половині сторони, до якої вона проведена, то це медіана прямокутного трикутника, проведена до гіпотенузи.
В прямокутному трикутнику сума гострих кутів дорівнює 90°, тобто прямий кут дорівнює сумі двох інших.
Доведено.
Автор ответа:
1
***
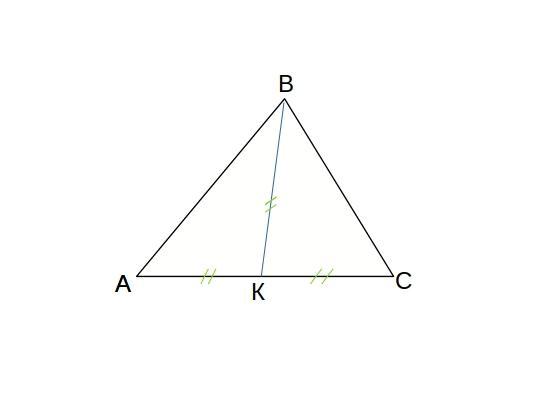
поскольку ВD-медиана
АD = DС = 1/2 · АС
⇔
треугольник АВK равнобедренный,
∠А = ∠ABK
значит:
треугольник KВС равнобедренный
∠С = ∠KВС
∠В = ∠АВK + ∠KВС = ∠А + ∠С
доказано.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: shaninaoksana2
Предмет: Английский язык,
автор: velikanovaevge1
Предмет: Английский язык,
автор: АняG27
Предмет: Английский язык,
автор: ignat0365