Question

100 баллов! срочно! решить неравенство, следуя алгоритму.
1. Привести неравенство к виду f(x)>0, или f(x)<0.
2. Найти D(f).
3. Найти нули функции f(x), решив уравнение f(x)=0.
4. Обозначить нули функции и найти знаки функции на каждом из промежутков, на которые разбито D(f).
5. Записать ответ, учитывая знак неравенства
$\sqrt{x + 3} > \sqrt{2x - 1} + \sqrt{x - 1}$
​

Answer 1

√(х+3) >√(2х-1)+ √(х-1).

2)D(f)

{x+3≥ 0,

{2x-1≥ 0,

{x-1≥0. Общее решение данной системы x≥ 1.

1) Возводим обе части в квадрат , тк левая и правые части положительны

х+3>2х-1+2√(2х-1)*√(х-1)+х-1,

5-2х>2√(2х²-3х+1). После возведения в квадрат получаем

25-20х+4 х²> 8х²-12х+4,

4х² +8х-21<0.

3)Нули функции f=4х² +8х-21.

4х² +8х-21=0 ,D=400, x1=1,5 , x2=-3,5.

Тогда 4(х-1,5)(х+3,5)<0

4)Найдем знаки функции на [1;+беск).

Значение -3,5∉[1;+беск).

4(х-1,5)(х+3,5)<0

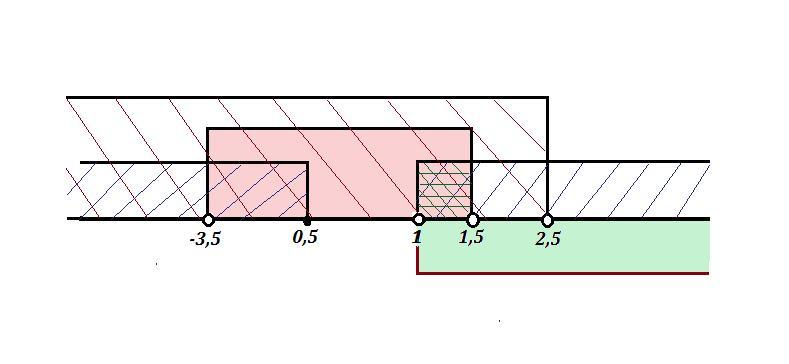
_______[1] - - - - [1,5]+ + +

Определим знак последнего интервала f(2)=4*2²+8*2-21=11>0. На этом интервале ставим знак «+».

5) Ответ. [1;1,5]

Answer 2

Ответ:

$\sqrt{x+3} > \sqrt{2x-1}+\sqrt{x-1}\\\\ODZ:\left\{\begin{array}{l}x+3\geq 0\\2x-1\geq 0\\x-1\geq 0\end{array}\right\ \ \left\{\begin{array}{l}x\geq -3\\x\geq 0,5\\x\geq 1\end{array}\right\ \ \ \Rightarrow \ \ \ \ x\in [\ 1\ ;+\infty \, )$  

Так как правая и левая части неравенства неотрицательны, то можно его возвести в квадрат .

$(x+3) > (2x-1)+2\sqrt{(2x-1)(x-1)}+(x-1)\\\\2\sqrt{(2x-1)(x-1)} < x+3-2x+1-x+1\\\\2\sqrt{(2x-1)(x-1)} < 5-2x\ \ \ \Longleftrightarrow \ \ \ \left\{\begin{array}{l}(2x-1)(x-1)\geq 0\\5-2x > 0\\4(2x-1)(x-1) < 25-20x+4x^2\end{array}\right$  

$\left\{\begin{array}{l}2(x-0,5)(x-1)\geq 0\\x < 2,5\\4x^2+8x-21 < 0\end{array}\right\ \ \left\{\begin{array}{l}2(x-0,5)(x-1)\geq 0\\x < 2,5\\4(x+3,5)(x-1,5) < 0\end{array}\right$  

$\star \ \ 4x^2+8x-21=0\ \ ,\ \ D/4=(b/2)^2-ac=16+84=100\ ,\\\\x_1=\dfrac{-4-10}{4}=-3,5\ \ ,\ \ \ x_2=\dfrac{-4+10}{4}=1,5\\\\4(x+3,5)(x-1,5) < 0$

Метод интервалов решения неравенств .

Знаки функции:   $+++(-3,5)---(1,5)+++$  

$f(100)=4(100+3,5)(100-1,5) > 0\\\\f(0)=4(0+3,5)(0-1,5) < 0\\\\f(-100)=4(-100+3,5)(-100-1,5) > 0$  

Выбираем интервал, где записан знак минус :  $\boldsymbol{x\in (\, -3,5\ ;\ 1,5\ )}$  .

$\star \ \ 2(x-0,5)(x-1)\geq 0\\\\znaki:\ \ \ +++[\ 0,5\, ]---[\ 1\ ]+++\ \ ,\ \ \ \boldsymbol{x\in (-\infty ;\, 0,5\ ]\cup [\ 1\ ;+\infty )}\ \ \star$

$a)\ \ \left\{\begin{array}{l}x\in (\, -3,5\ ;\ 1,5\ )\\x < 2,5\\x\in (-\infty ;\, 0,5\ ]\cup [\ 1\ ;+\infty )\end{array}\right\ \ \ \ \Rightarrow \ \ \ \ \boldsymbol{x\in (-3,5\ ;\ 0,5\ ]\cup (\ 1\ ;\ 1,5\ )}\\\\\\b)\ \ \left\{\begin{array}{l}x\in (-3,5\ ;\ 0,5\ ]\cup (\ 1\ ;\ 1,5\ )\\x\in [\ 1\ ;+\infty \, )\end{array}\right\ \ \ \ \ \Rightarrow \ \ \ \boldsymbol{x\in (\ 1\ ;\ 1,5\ )}\\\\\\Otvet:\ \ \boldsymbol{x\in (\ 1\ ;\ 1,5\ )}\ .$