Предмет: Математика,
автор: 0001001
задание по математике
Приложения:
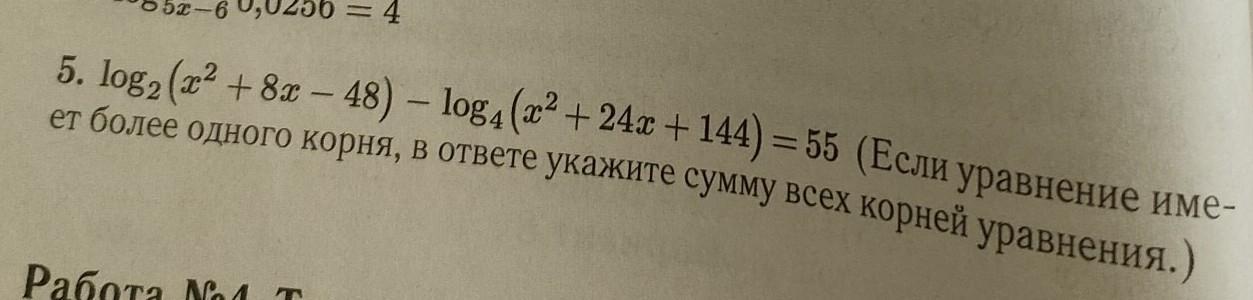
Ответы
Автор ответа:
0
Ответ:
x₁ + x₂ = 2⁵⁵+ 2⁻⁵⁵ + 8
Пошаговое объяснение:
ОДЗ :
/////// ///////
Для | x + 12 | ОДЗ не нужно , т.к при любом значении оно будет больше нуля , либо равно нулю , и в промежутке уже указано что
x ≠ 12
Тогда
В указанных промежутках
x может быть меньше -12 , и также больше -12
Поэтому модуль можно раскрыть с плюсом и также с минусом
Тогда
При x > -12
При x < -12
Похожие вопросы
Предмет: Русский язык,
автор: yangulova
Предмет: Қазақ тiлi,
автор: turetaevameruer
Предмет: Русский язык,
автор: Deni250
Предмет: Геометрия,
автор: qweryuio123456
Предмет: География,
автор: ermak1234