Question

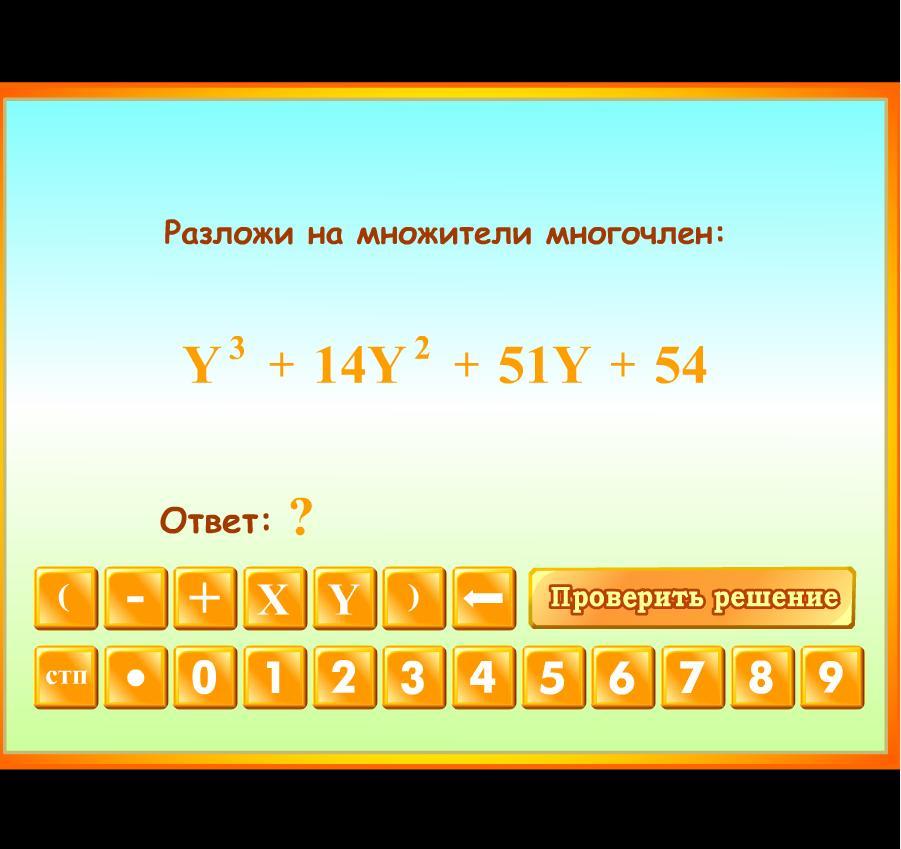
Разложи на множители многочлен

Answer 1

Ответ:

Чтобы разложить многочлен на множители, найдём его корни, решим уравнение

$y^3+14y^2+51y+54=0$  

Первый корень подберём среди делителей свободного члена, числа 54 . Это будет х= -2 , так как

$(-2)^3+14(-2)^2-51\cdot 2+54=-8+56-102+54=0$  

Значит многочлен нацело разделится на (y+2) . Выделим этот множитель в многочлене.

$y^3+14y^2+51y+54=(y^3+\underbrace{2y^2)+(12y^2}_{14y^2}+\underbrace{24y)+(27y}_{51y}+54)=\\\\=y^2(y+2)+12y(y+2)+27(y+2)=(y+2)(y^2+12y+27)\ ;$  

Теперь найдём корни квадратного трёхчлена по теореме Виета .

$y^2+12y+27=0\ \ ,\ \ y_1=-3\ ,\ y_2=-9$  

Тогда   $y^2+12y+27=(y+3)(y+9)$  .

Окончательно получаем

$\boldsymbol{y^3+14y^2+51y+54=(y+2)(y+3)(y+9)}$