Предмет: Алгебра,
автор: golovanovairina848
помогите с решением!!)!) срочно
полное решение
Приложения:
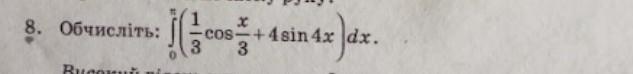
Ответы
Автор ответа:
2
Ответ:
Объяснение:
Найдем неопределенный интеграл
Находим наш определенный интеграл
Похожие вопросы
Предмет: Английский язык,
автор: papimilk
Предмет: Русский язык,
автор: Aрeтмка
Предмет: Окружающий мир,
автор: AliceLemur
Предмет: Литература,
автор: katepodruga
Предмет: История,
автор: DenisFazbear