Предмет: Геометрия,
автор: networkedloner
Кут при основі рівнобедреного трикутника дорівнює 30градусів. Радіус кола, описаного навколо трикутника, дорівнює 4 см. Визначити радіус кола, вписаного в даний трикутник.
Ответы
Автор ответа:
2
Ответ: см .
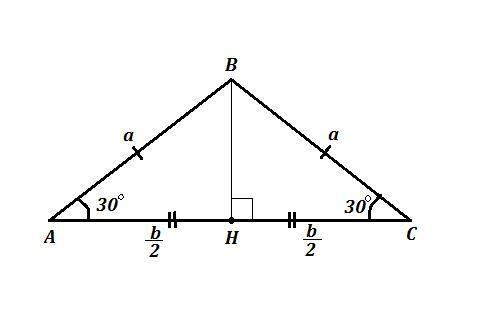
ΔАВС - равнобедренный , АВ=ВС . ∠А=∠С=30° . R - радиус описанной окружности , r - радиус вписанной окружности , R=4 cм . Найти: r .
По теореме синусов имеем
см .
Опустим перпендикуляр ВН из вершины В на основание АС . Точка Н будет серединой основания АС .
Найдём АН из ΔABH .
см
Тогда м .
Известна формула площади треугольника через радиус вписанной окружности : , где р - полупериметр . Отсюда можно выразить радиус вписан. окр-ти
.
Найдём полупериметр ΔABС .
см .
Теперь найдём площадь треугольника АВС .
см²
см
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Alekc5193
Предмет: Қазақ тiлi,
автор: сузыкпаевадана
Предмет: Русский язык,
автор: sabinasabirova1
Предмет: Математика,
автор: LeraLusheva
Предмет: Информатика,
автор: nyashagg