Question

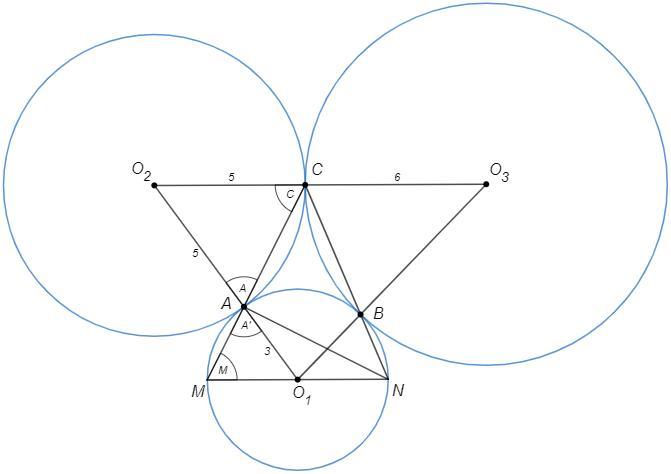
Первая окружность касается второй и третьей в различных точках A и B соответственно а вторая и третья касаются друг друга вточке C прямые AC и BC пересекают первую окружность в точках ответ M и N соответственно А) докажите что отрезок MN являются диаметром первой окружности Б) радиусы первой, второй и третьей окружностей равны 3,5 и 6 соответственно Найдите площадь треугольника AMN​

Answer 1

а) △AO1M, △AO2C - р/б => ∠C=∠A=∠A'=∠M => O1M||O2C

Аналогично O1N||O3C

Точка касания лежит на линии центров, O2-C-O3 на одной прямой

=> M-O1-N на одной прямой, MN - диаметр

б) Рассмотрим △O1O2O3

Стороны равны сумме радиусов: 8, 9, 11

Площадь по формуле Герона

p= (8+9+11)/2 =14

S= √(14*6*5*3) =6√35

Площади треугольников с равным углом относятся как произведения сторон.

S(AO2C)/S(O1O2O3) =5*5/8*11 => S(AO2C) =25/88 *6√35

△AO1M~△AO2C, k=3/5

Площади подобных фигур относятся как квадрат коэффициента подобия.

S(AO1M)/S(AO2C) =9/25 => S(AO1M) =9/88 *6√35

S(AMN) =2S(AO1M) (AO1 - медиана) =2 *9/88 *6√35 =27/22 *√35  ~7,26