Предмет: Алгебра,
автор: Kirofeed
Помогите решить! Задача для школьников, то есть метод математической индукции нужно как-то обойти.
Приложения:
BMW52:
470838
Неверно.
может разбить на несколько сумм?
Ответы
Автор ответа:
1
Ответ:
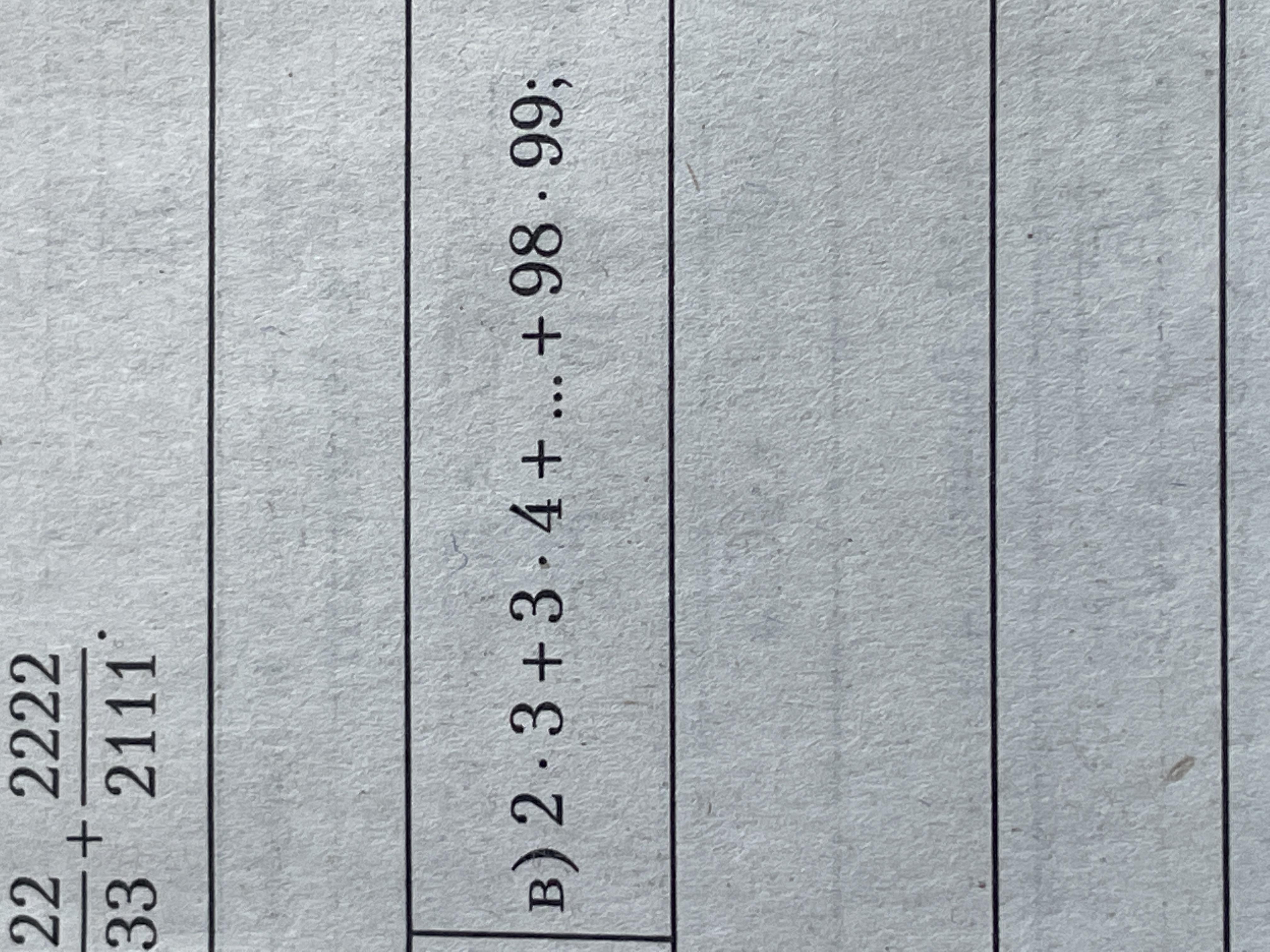
2·3 + 3·4 + ... + 98·99 = 323398
Объяснение:
Заметим что
Выходит арифметическая прогреcсия , а также сумма квадратов чисел от 3 до 99
Для арифметической прогрессии все просто
А сумму квадратов чисел от 3 до 99 , найдем с помощью формулы
( n - количество чисел от 1² + 2² ... + n²)
Но наш ряд начинается с тройки , поэтому нужно отнять 1² + 2² = 5
Теперь находим
#SPJ1
Похожие вопросы
Предмет: Русский язык,
автор: mcxovanskiy11
Предмет: Қазақ тiлi,
автор: нурланнурару
Предмет: Другие предметы,
автор: мирана23
Предмет: География,
автор: FrolovVasia
Предмет: Русский язык,
автор: 12commikoazru