Подскажите пж дам 20 балов!!
Ответы
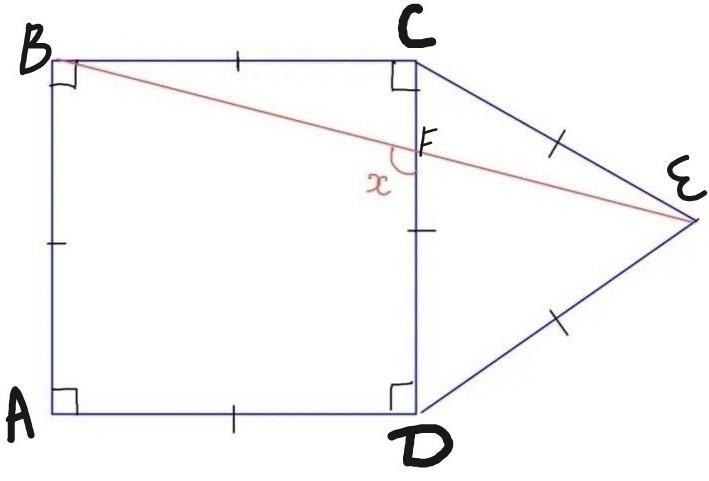
Дивiться фото. <DCE=60° (за вл. рiвност. тр.) => <ВСЕ=90°+60°=150° (за аксiомою вим. кутiв); ВС=СЕ => трикутник ВСЕ — рiвнобедрений => <СВЕ=<СЕВ=(180°-150°)/2=30°/2=15°. Розгл. тр. ВСF <BCF=90° => <CFB=90°-15°=75°(за т. про суму гострих кутiв прям. тр.) => <ВFD=180°-75°=105°(як сумiжнi).
Вiдповiдь: 105°.
Ответ:
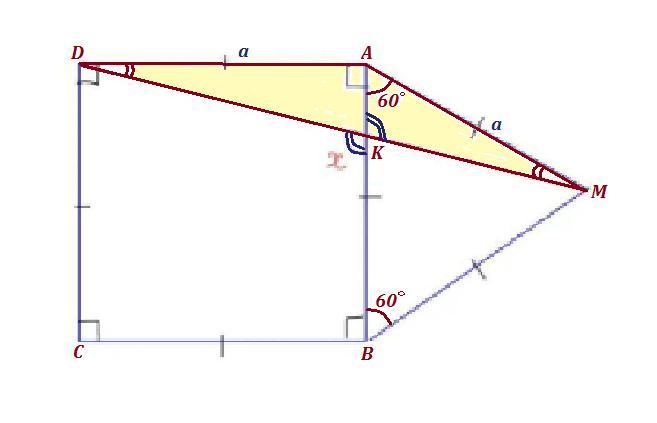
ABCD - квадрат , ΔАМВ - равносторонний, значит все его углы равны 60° . Стороны квадрата равны сторонам правильного треугольника .
∠ВАМ=60° , ∠DAM=∠DAB+∠BAM=90°+60°=150°
ΔDAM - равнобедренный, так как АD=АМ , с углом при вершине, равным ∠DAM=150° . Тогда углы при основании этого треугольника равны и ∠ADM=∠AMD=(180°-150°):2=30°:2=15°
Рассмотрим ΔAMK . В этом треугольнике известны два угла: ∠МАК=60° и ∠АМК=15° .
Сумма углов треугольника равна 180° , поэтому третий угол в ΔАМК равен ∠АКМ=180°-(60°+15°)=180°-75°=105° .
Но ∠АКМ и ∠х=∠ВКD - вертикальные. А значит они равны между собой . Поэтому ∠х=105° .