Предмет: Алгебра,
автор: muhammedsurname8
решите совокупность неравенств
Приложения:
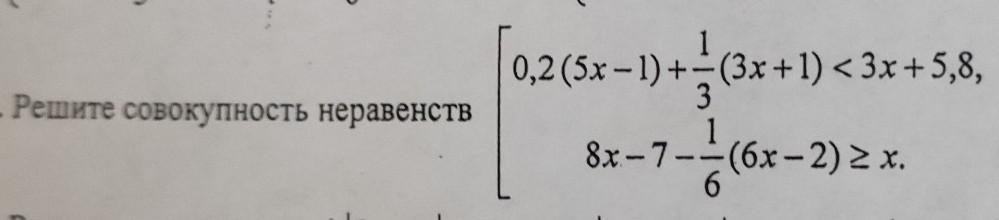
Ответы
Автор ответа:
3
Ответ:
Ответ:
Объяснение:
Решить совокупность неравенств:
Решим каждое неравенство отдельно, а в ответ запишем все решения данных неравенств.
1. Решим первое неравенство.
Раскроем скобки. Перенесем неизвестные влево, известные вправо. Не забываем при переносе через знак неравенства поменять знаки на противоположные.
Приведем подобные члены:
- Если обе части неравенства умножить или разделить на отрицательное число, то знак неравенства перевернется.
2. Аналогично решим второе неравенство.
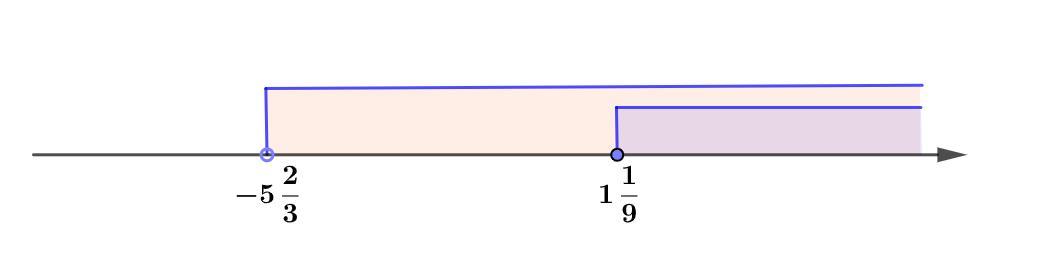
Отметим решения на числовой оси и объединим промежутки.
См. рис.
Получили ответ:
#SPJ1
Приложения:
muhammedsurname8:
спасибо большое
Похожие вопросы
Предмет: Русский язык,
автор: пит286
Предмет: Русский язык,
автор: katyasalikhova
Предмет: Русский язык,
автор: DipperMystic
Предмет: Физика,
автор: amirkosta47
Предмет: Окружающий мир,
автор: kuraevasvetlana