Question

СРОЧНО
Основою прямої призми є ромб із гострим кутом а. Через меншу діагональ нижньої основи та вершину гострого кута верхньої основи проведено площину, яка утворює з площиною основи кут В. Знайдіть площу бічної поверхні призми, якщо менша діагональ її основи дорівнює d.​

Answer 1

Ответ:

Площадь боковой поверхности призмы равна  $\displaystyle \bf\frac{d^2\;cos\frac{\alpha }{2}\;tg\beta }{sin^2\frac{\alpha }{2} }$.

Объяснение:

Основой прямой призмы является ромб с острым углом α. Через меньшую диагональ нижнего основания и вершину острого угла верхнего основания проведена плоскость, которая образует с плоскостью основания угол β. Найдите площадь боковой поверхности призмы, если меньшая диагональ ее основания равна d.​

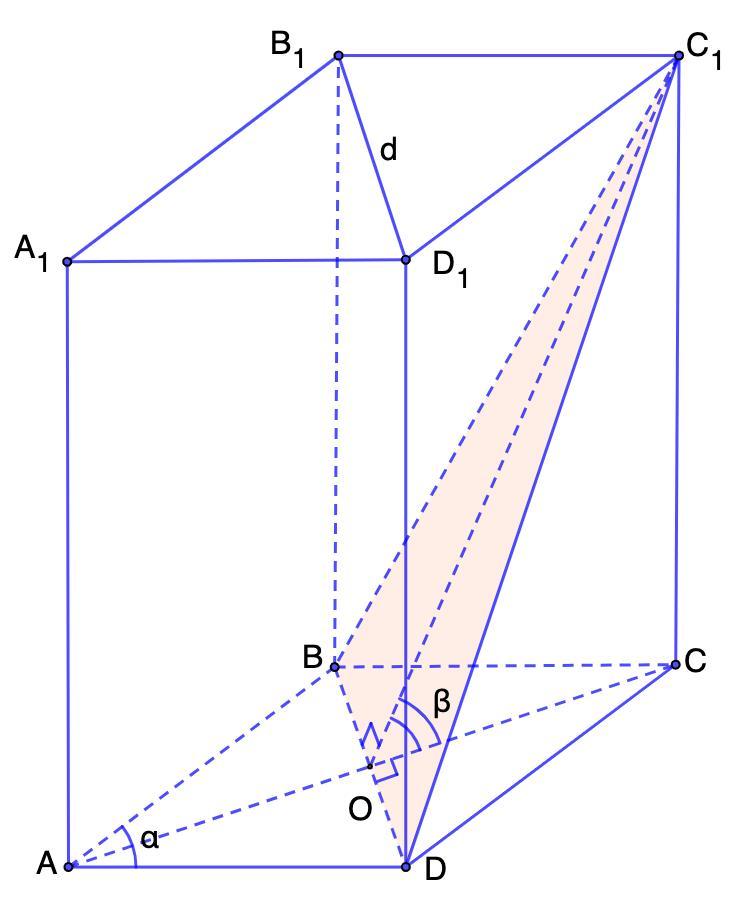
Дано: ABCDA₁B₁C₁D₁ - прямая призма.

ABCD - ромб;

ВС₁D - сечение;

∠А = α;

угол между сечением и основанием равен β;

BD = d.

Найти: Sбок.

Решение:

Площадь боковой поверхности прямой призмы равна:

         $\displaystyle \bf \boxed {S_{bok}=P_{osn}\cdot{h}}$ ,

где Росн - периметр основания, h - высота призмы.

• Прямая призма — это призма, у которой боковые рёбра перпендикулярны плоскости основания и все боковые грани являются прямоугольниками.

Найдем периметр основания. Он будет равен:

Росн = 4а, где а - сторона основания.

1. Рассмотрим ABCD - ромб.

• Диагонали ромба взаимно перпендикулярны.

⇒ AC ⊥ BD;

• Диагонали ромба точкой пересечения делятся пополам.

⇒ BO = OD; AO = OC.

• Диагонали ромба являются биссектрисами углов.

⇒ ∠ВАО = ∠ОАD.

2. Рассмотрим ΔАВО - прямоугольный.

∠ВАО = α/2;

• Синус угла - отношение противолежащего катета к гипотенузе.

⇒

$\displaystyle \bf sin\frac{\alpha }{2}=\frac{OB}{AB} \\\\OB=\frac{d}{2}\\ \\AB=\frac{OB}{sin\frac{\alpha }{2} } =\frac{d}{2sin\frac{\alpha }{2} }$

Периметр основания равен:

$\displaystyle \bf P_{osn}=4\cdot{\frac{d\;}{2sin\frac{\alpha }{2} } }=\frac{2d}{sin\frac{\alpha }{2} }$

Так же из этого треугольника выразим АО.

• Косинус угла - отношение прилежащего катета к гипотенузе.

$\displaystyle \bf cos\frac{\alpha }{2}=\frac{AO}{AB} \\\\AO=AB\;cos\frac{\alpha }{2}=\frac{d}{2sin\frac{\alpha }{2} } \cdot{cos\frac{\alpha }{2} }=\frac{d\;cos\frac{\alpha }{2} }{2sin\frac{\alpha }{2} }$

Периметр основания нашли, осталось найти высоту.

3. CO⊥ BD.

• Теорема о трех перпендикулярах: прямая, проведенная в плоскости через основание наклонной перпендикулярно к ее проекции на эту плоскость, перпендикулярна и к самой наклонной.

⇒ С₁О ⊥ BD.

⇒ ∠C₁OC = β - угол между сечением и основанием.

4. Рассмотрим ΔОС₁С - прямоугольный.

$\displaystyle \bf CO = AO = \frac{d\;cos\frac{\alpha }{2} }{2sin\frac{\alpha }{2} }$

• Тангенс угла - отношение противолежащего катета к прилежащему.

$\displaystyle \bf tg\beta =\frac{CC_1}{CO}\\ \\CC_1=CO\;tg\beta =\frac{d\;cos\frac{\alpha }{2}\;tg\beta }{2sin\frac{\alpha }{2} }$

5. Теперь найдем площадь боковой поверхности.

$\displaystyle \bf S_{bok}=\frac{2d}{sin\frac{\alpha }{2} } \cdot\frac{d\;cos\frac{\alpha }{2}\;tg\beta }{2sin\frac{\alpha }{2} } =\frac{d^2\;cos\frac{\alpha }{2}\;tg\beta }{sin^2\frac{\alpha }{2} }$

Площадь боковой поверхности призмы равна  $\displaystyle \bf\frac{d^2\;cos\frac{\alpha }{2}\;tg\beta }{sin^2\frac{\alpha }{2} }$.

#SPJ1