Предмет: Геометрия,
автор: alesazezulina041
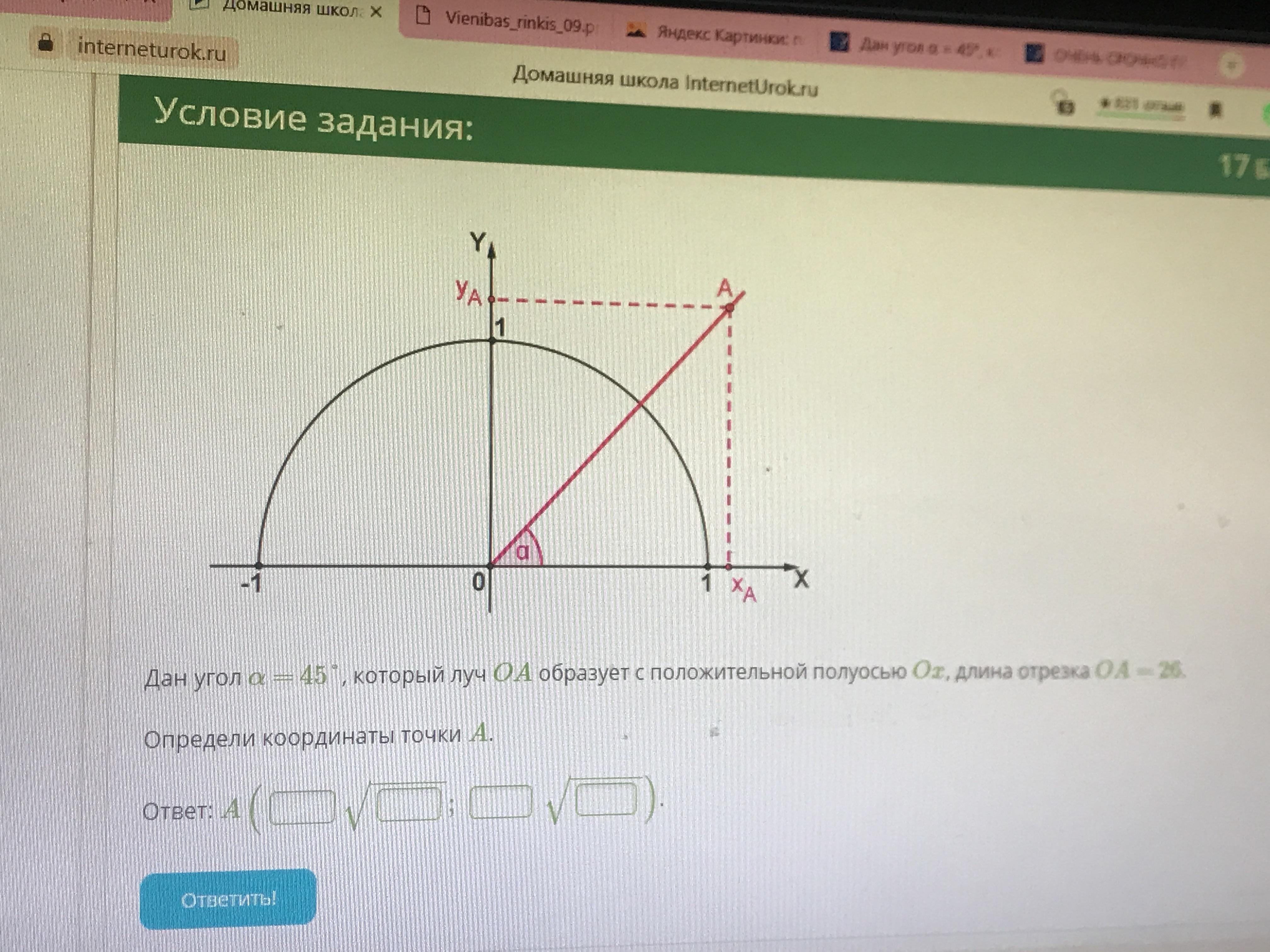
ГЕОМЕТРИЯ 70 БАЛЛОВ СРОЧНО ПОЖАЛЦЙСТА !!!
Приложения:
Ответы
Автор ответа:
3
Ответ:
Объяснение:
Треугольник является прямоугольно-равнобедренным ⇒
По теореме Пифагора
Ордината точки равна нулю , теперь чтобы найти ее абсциссу
воспользуемся формулой
где - расстояние между точками
В нашем случае
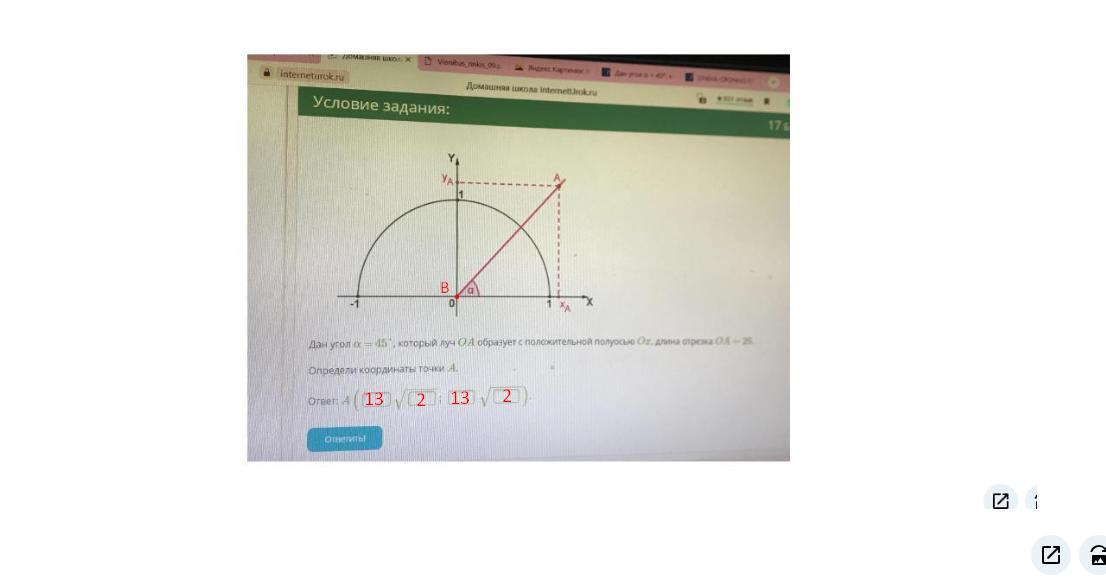
Мы нашли координаты точки
А чтобы найти координаты точки A
Нужно к ординате точки добавить
Приложения:
zmeura1204:
13√2
Похожие вопросы
Предмет: Русский язык,
автор: ислам281
Предмет: Русский язык,
автор: temik3061genius
Предмет: Русский язык,
автор: inessa2012
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: vityazinovev94