Question

100 баллов! срочно! решить уравнение. с подробным пошаговым решением!
$\sqrt[8]{x} + \sqrt[5]{x} = \frac{2}{x}$
​

Answer 1

Ответ:

!!!!!!!!!!!!!!!!!

Объяснение:

Answer 2

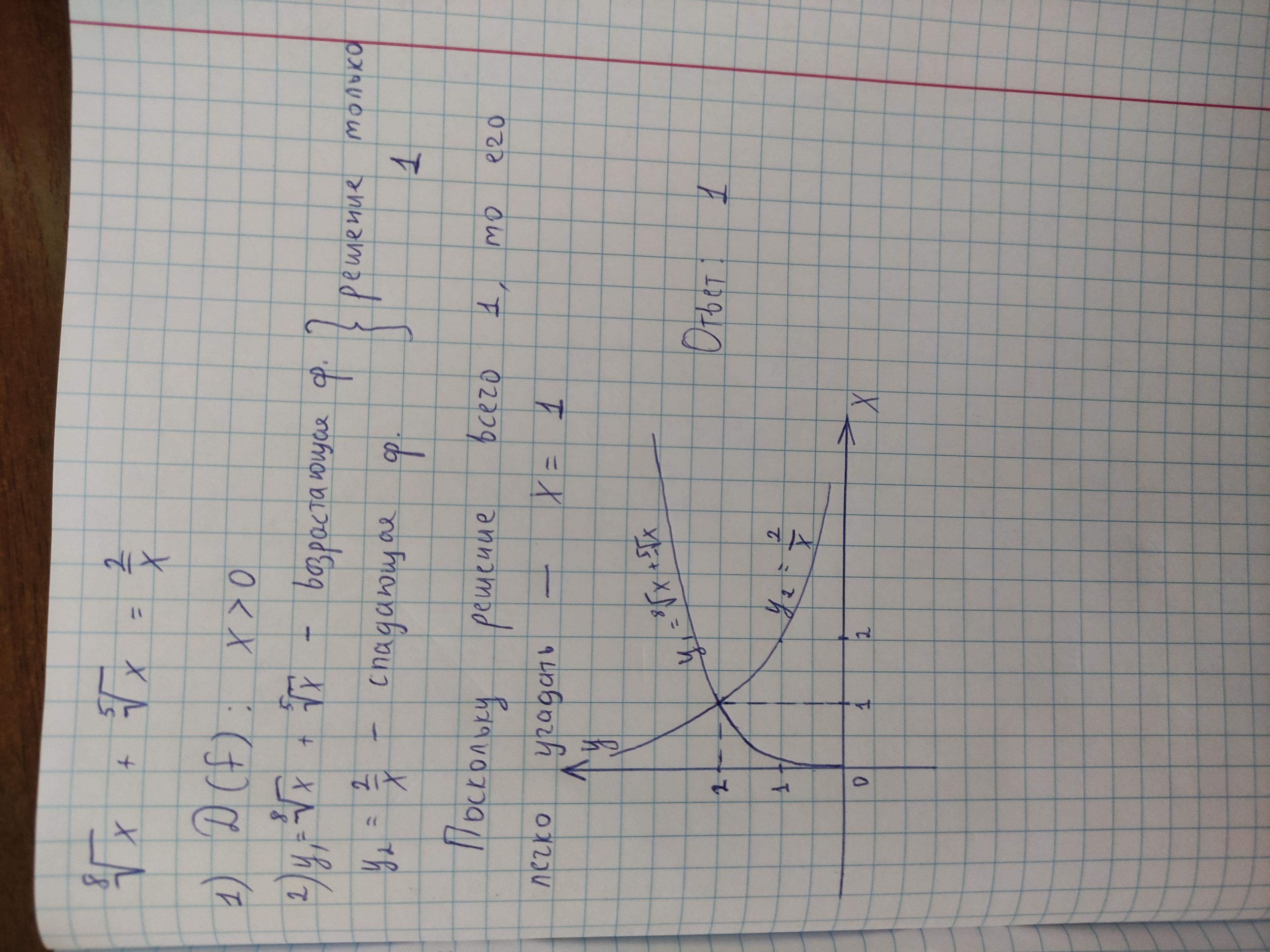
Ответ:

x=1.

Объяснение:

если комбинировать методы, можно решить таким путём:

1) ОДЗ уравнения базируется на дроби (х≠0) и на корне чётной степени (х≥0), то есть только положительные значения Х являются допустимыми в данном уравнении;

2) левая часть исходного уравнения представляет из себя одну ветви параболы, которая лежит в первой координатной четверти; правая же часть - гиперболу, ветви которой лежат в первой и третьей четвертях. Как вывод: при таких графиках только одна точка пересечения, то есть только один корень;

3) если в исходном уравнении сделать замены вида

$x=t^{40}; \sqrt[8]{x}=t^5; \sqrt[5]{x}=t^8,$

тогда исходное уравнение (ОДЗ: только положительные числа) становится таким:

$t^{48}+t^{45}-2=0;$

где элементарным подбором видно (теорема Безу), что t=1;

4) если понижать степень в уравнении пункта №3, тогда получается, что

$(t-1)(t^{47}+t^{46}+t^{45}+2t^{44}+2t^{43}+...+2t+2)=0;$

дальнейшее понижение степени полинома 47-й степени не есть целесообразно, так как согласно пункту №2 уравнение имеет единственный действительный корень. Это х=1.