Предмет: Алгебра,
автор: arinaduruan
Помогите решить пожалуйста
Приложения:
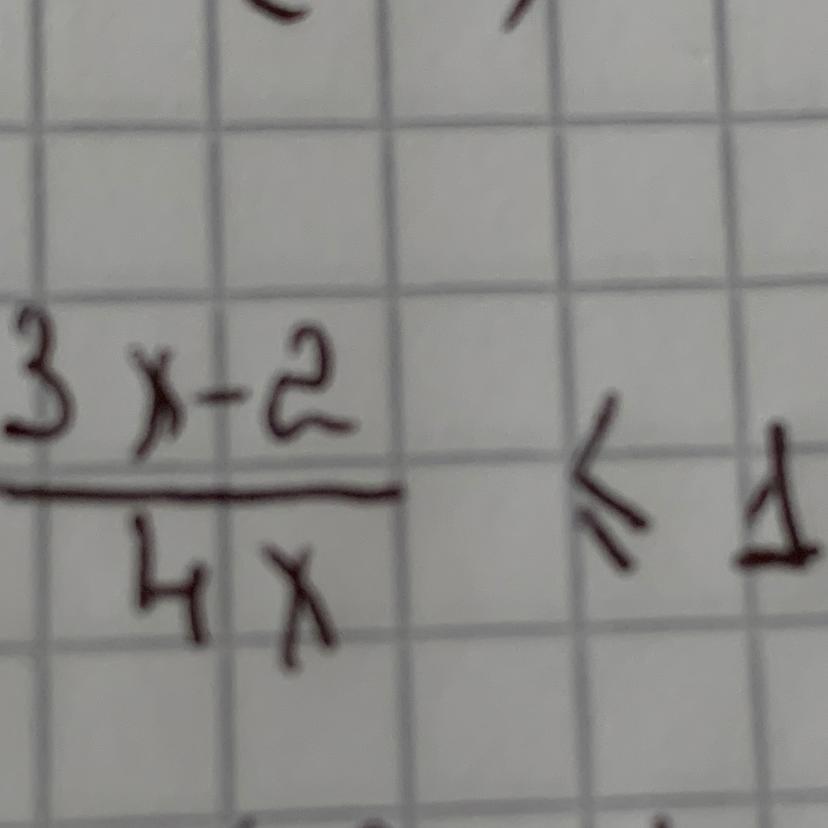
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Автор ответа:
0
Объяснение:
(3х - 2)/4х ≤ 1, x ≠ 0
(3х - 2)/(4х) - 1 ≤ 0
(3х - 2 - 4х)/4х ≤ 0
(-х - 2)/4х ≤ 0
{-х - 2 ≤ 0
{4х > 0
{-х - 2 ≥ 0
{4х < 0
{х ≥ -2
{х > 0
{х ≤ -2
{х < 0
х Є (0, +∞)
х Є (-∞, -2]
х Є (-∞, -2] U (0, +∞), x ≠ 0
Ответ: х Є (-∞, -2] U (0, +∞)
Похожие вопросы
Предмет: Русский язык,
автор: labisamursalov27
Предмет: Русский язык,
автор: 2007200774825
Предмет: Английский язык,
автор: лалаьк
Предмет: Информатика,
автор: NeksusPRO
Предмет: Алгебра,
автор: volkogonboris