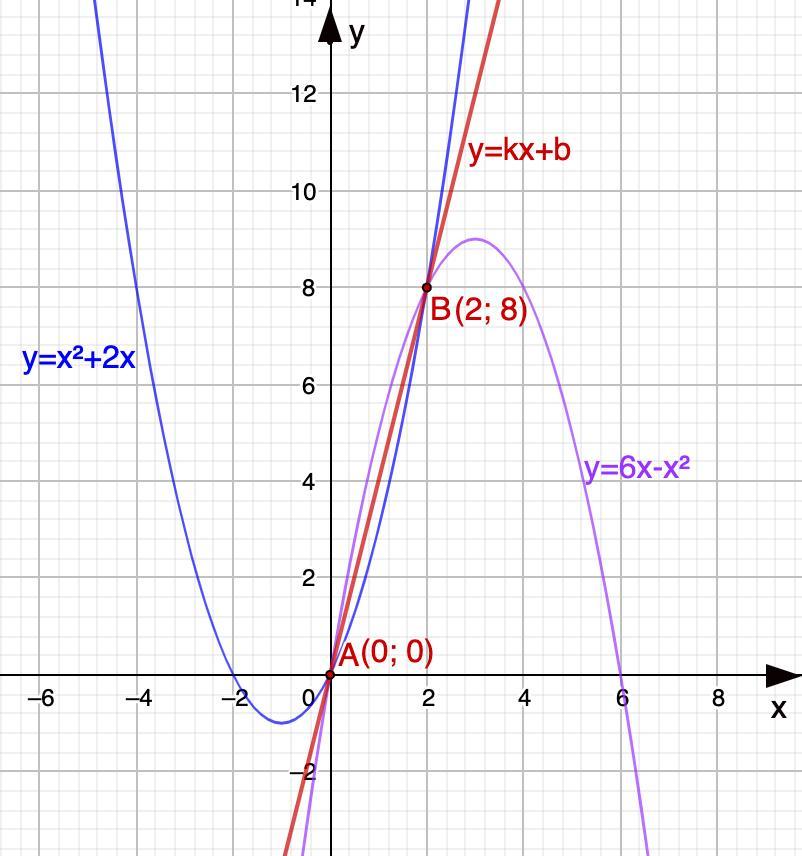
Даю 40 баллов. Задача на фото:
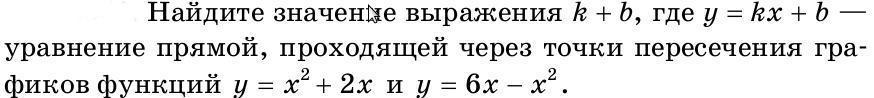
Ответы
Ответ:
k + b = 4
Пошаговое объяснение:
Найдем точки пересечения графиков функций
у = x² +2x
y = 6x - x²
Координаты точек пересечения должны удовлетворять обоим уравнениям .
Поэтому, чтобы найти координаты точек пересечения решим уравнение.
x² +2x = 6x - x²
2x² -4x = 0
2x( x - 2) =0 ⇒ x₁ = 0; x₂ = 2
Найдем координату у
x₁ = 0; у₁ = x² +2x; у₁ = 0² +2*0; y₁ = 0
(0; 0) - это одна точка пересечения.
x₂ = 2; y₂ = x² +2x; y₂ = 2² + 2*2; y₂ = 8
(2; 8) - это вторая точка пересечения.
Теперь надо написать уравнение прямой, проходящей через две точки.
Можно, конечно, написать каноническое уравнение прямой, а потом из него получить уравнение с угловым коэффициентом.
Но мы порассуждаем.
Если график проходит через точку (0; 0), то коэффициент b =0
0 = k*0 + b ⇒ b =0
Теперь используем вторую точку. Подставим ее координаты в уравнение
8 = k*2 + 0 ⇒ k = 4
Таким образом, мы получили уравнение прямой
у = 4х
Ответ на вопрос задачи : k + b = 4 + 0 = 4
Ответ:
Значение выражения k + b равно 4.
Пошаговое объяснение:
Найдите значение выражения k + b, где y = kx + b - уравнение прямой, проходящей через точки пересечения графиков функций
у = х² + 2х и у = 6х - х²
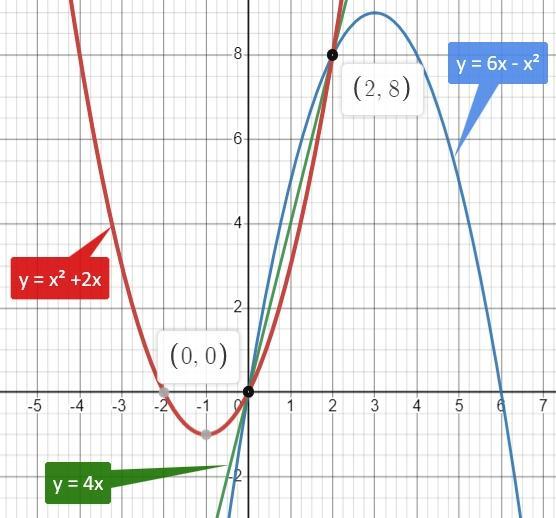
Искомый график проходит через точки пересечения графиков двух функций:
у = х² + 2х и у = 6х - х²
Найдем эти точки, решив систему уравнений:
Подставим значения х в любое из уравнений и найдем значения у:
Мы нашли две точки пересечения графиков: А(0; 0) и В(2; 8).
Эти точки принадлежат искомому графику.
- Если точка принадлежит графику, то, подставив ее координаты в уравнение функции, получим верное равенство.
Подставим координаты точек в уравнение у = kx + b и решим систему уравнений:
Получили уравнение прямой:
у = 4x
Значение выражения k + b равно 4.