Предмет: Геометрия, автор: teacherGeometrie

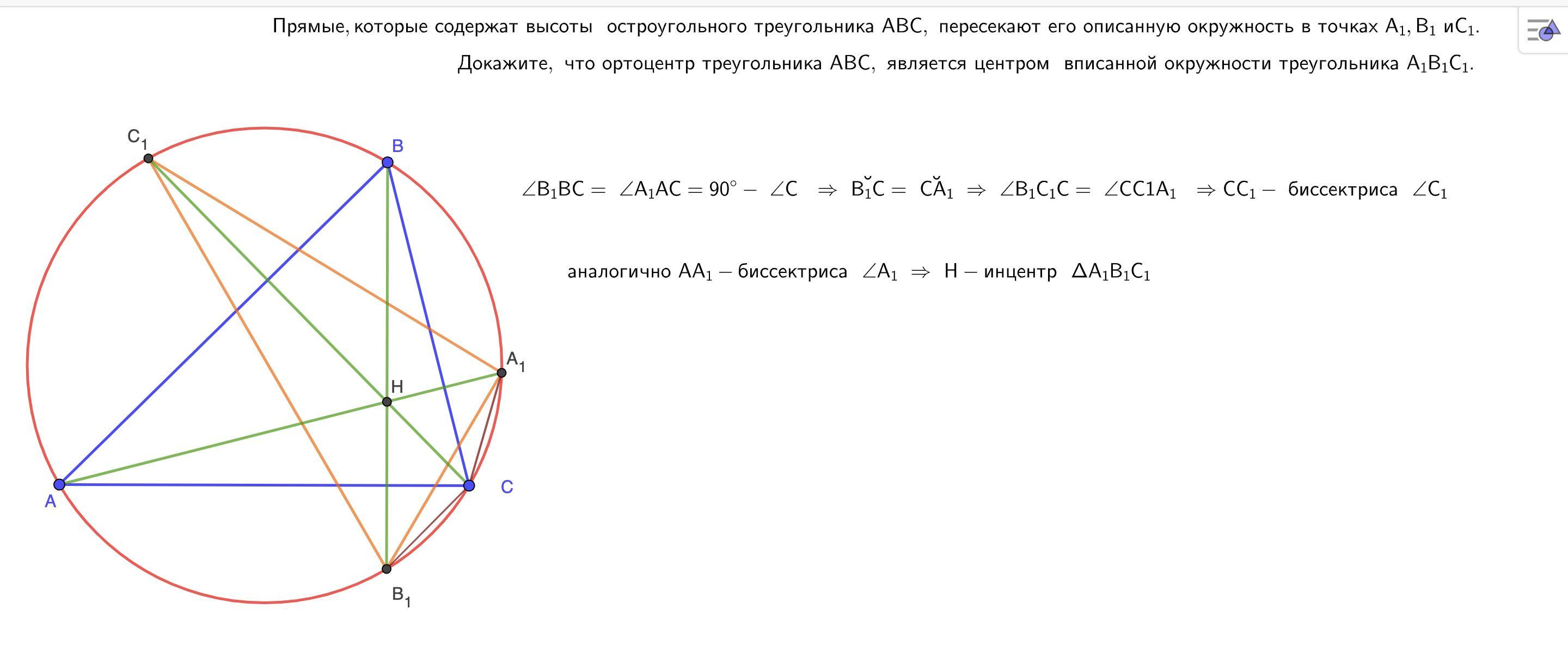
Прямые, которые содержат высота остроугольного треугольника АВС, пересекают его описанную окружность в точках А1, В1 и С1. Докажите, что ортоцентр треугольника АВС, является центром вписанной окужности треугольника А1В1С1.

teacherGeometrie: На всякий случай скажу: ортоцентр - это точка пересечения высот.

antonovm: высоты треугольника - биссектрисы ортотреугольника ( легко доказывается через вспомогательные окружности ) , а точка пересечения биссектрис - центр вписанной окружности

antonovm: невнимательно прочёл , это не ортотреугольник , но из параллельности сторон ортотреугольника сторонам треугольника A1B1C1 следует это утверждение

teacherGeometrie: Простите, но я что-то не очень понял - а где здесь ортотреугольник?

teacherGeometrie: В задачи дан треугольник, у которого высоты пересекают окружность в точках А1 В1 С1.

antonovm: лучше я решение напишу ( чуть позже ) и всё станет ясно

antonovm: "Не грусти, — сказала Алисa. — Рано или поздно все станет понятно, все станет на свои места и выстроится в единую красивую схему, как кружева. Станет понятно, зачем все было нужно, потому что все будет правильно."

antonovm: А в самом деле , ну зачем нужен ортотреугольник , задача - то устная , чуть позже второй вариант решения напишу

antonovm: добавил второй вариант , ну конечно она устная