Предмет: Геометрия,
автор: irinamahige
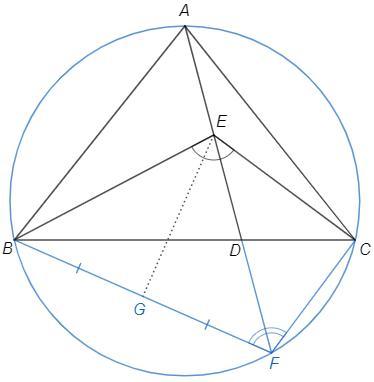
ABC - треугольник, в котором АВ = АС. D - точка на стороне BC и Е - точка на отрезке AD. Угол BED равен углу BAC и равен удвоенному углу DEC. Доказать, что DB = 2×CD. Помогите, пожалуйста.
Ответы
Автор ответа:
2
На продолжении AD возьмем точку E, BE=EF
△BAC~△BEF (р/б, ∠BAC=∠BED)
BA/BE=BC/BF
∠ABC=∠EBF => ∠ABE=∠CBF
△ABE~△CBF (по двум пропорциональным сторонам и углу между ними)
∠BAF=∠BCF, отрезок BF виден из точек A и C под равным углом
=> BACF - вписанный
∠AFB=∠AFC (опираются на равные хорды)
EG - биссектриса/медиана в △BEF
∠FEG=∠BED/2=∠DEC
△FEG =△FEC (по стороне и прилежащим углам) => FG=FC => BF=2FC
BD/DC=BF/FC=2/1 (BFC, по т о биссектрисе)
Приложения:
irinamahige:
Wow!!!
Здорово! Спасибо большое!
Я нажала как-то неправильно на звездочки и получилась оценка 1. Я хочу испавить на 5, но не получается. ☹️
Похожие вопросы
Предмет: Русский язык,
автор: НянКетNyanCat
Предмет: Английский язык,
автор: vladalogunova
Предмет: Русский язык,
автор: romahabibov
Предмет: Алгебра,
автор: Venus12
Предмет: Русский язык,
автор: Аноним