Предмет: Математика,
автор: ludmilastratij10
Знайти значення виразу
Приложения:
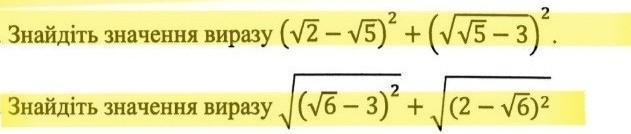
Ответы
Автор ответа:
1
Ответ:
1) 4-2√10+√5
2) 1
Пошаговое объяснение:
Пример №1
1. (√2-√5)²=2-2√10+5 (используя формулу (a-b)²)
2. (√√5-3)²=√5 - 3 (поднесли в квадрат, тем самым сократился первый большой корень)
3. 2-2√10+5+√5-3=4-2√10+√5
Пример №2
1. √(√6-3)²=3-√6 (поднесли в квадрат, тем самым сократился первый большой корень)
2. √(2-√6)²=|2-√6| (значение примера под корнем не может быть отрицательным, поэтому ставим модуль)
3. 3-√6+√6-2=1
brainly2949:
В 2 задание ошибка . Ви не поставили модуль ,а это нужно било заделать ,бо 2-✓6- выражение отрицательное ,нужно поставить модуль и Вынести (-) ,тогда будет -2+✓6,аналогично со 2.
Дякую, виправив!
Дуже банальна помилка, це моя слабкість)
К сожалению, во втором примере вы ошиблись
Я исправил же
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: Ангелина20062017
Предмет: Английский язык,
автор: приветик671
Предмет: Русский язык,
автор: serjsutyrin
Предмет: Химия,
автор: aliona12345
Предмет: Литература,
автор: ForestLopster