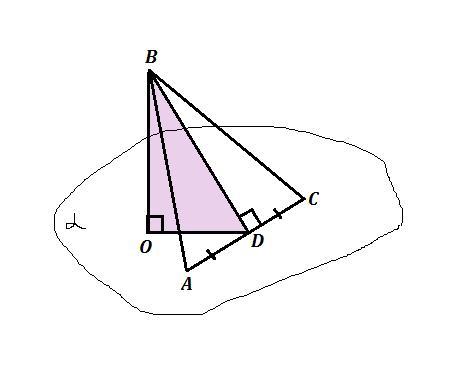
СРОЧНО!!! площина а проходить через основу АС рівнобедреного трикутника АВС .ВО перп а ,ВD висота,доведіть що пряма АС перпенд площині ВDO
Ответы
Ответ:
ΔАВС - равнобедренный , АВ=ВС , BD ⊥AC ,
ВО ⊥ плоскости α ⇒ ВО перпендикулярна любой прямой в плоскости α . Проведём прямую DО , тогда DО ⊥ BO и ΔВOD - прямоугольный , ∠BOD=90° . Тогда BD - наклонная , а DO - проекция наклонной BD на плоскость α .
BD ⊥ AC , так как BD - высота равнобедренного треугольника АВС .
По теореме о трёх перпендикулярах : если прямая, проведенная на плоскости через основание наклонной, перпендикулярна самой наклонной, то она перпендикулярна и её проекции .
Точка D - основание BD . Наклонная BD перпендикулярна прямой АС, тогда и её проекция DO перпендикулярна прямой AC.
Получили, что АС ⊥ BD и АС ⊥ DO . По признаку перпендикулярности прямой и плоскости, прямая АС будет перпендикулярна плоскости, в которой лежат прямые BD и DO , то есть плоскости BDO . Что и требовалось доказать .