Предмет: Математика,
автор: nazar228dino
Помогите решить: через точку К, лежащую на окружности, проведена касательная КМ. Найдите угол КОМ, если угол КМО равен 38°.
BMW52:
угол КОМ равен 90-38=52
при этом надо добавить, что касательная всегда перепендикулярна радиусу и поэтому угол МКО = 90 градусов. а сумма углов треугольника равна 180 градусов. поэтому два оставшихся угла КМО +МКО = 90 градусов. отсюда и выходит вышеуказанная формула.
"10"
Ответы
Автор ответа:
0
Ответ:
∠КОМ=52°
Пошаговое объяснение:
КМ - касательная к окружности с центром в точке О, К - точка касания.
КО - радиус окружности.
По свойству касательной: КО⊥КМ (Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания).
ΔКОМ - прямоугольный. ∠К=90°.
∠КОМ = 90°-∠КМО=90°-38°=52° - так как сумма острых углов прямоугольного треугольника равна 90°
Приложения:
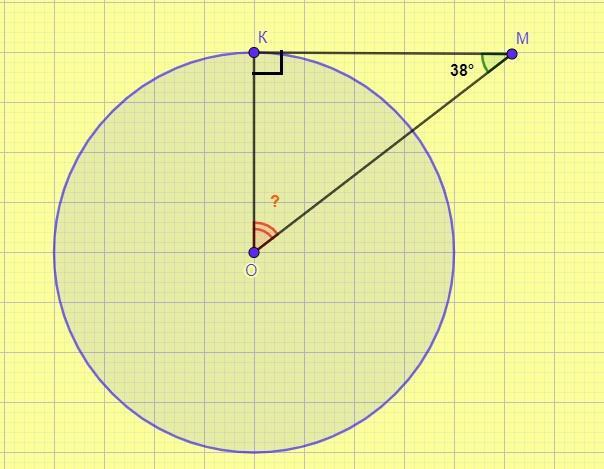
Чертёж классный.
Похожие вопросы
Предмет: Русский язык,
автор: katerina0061
Предмет: Русский язык,
автор: настя4816
Предмет: Русский язык,
автор: ГромкийНиндзя
Предмет: Биология,
автор: Аноним
Предмет: Английский язык,
автор: elmanselimov2001