Question

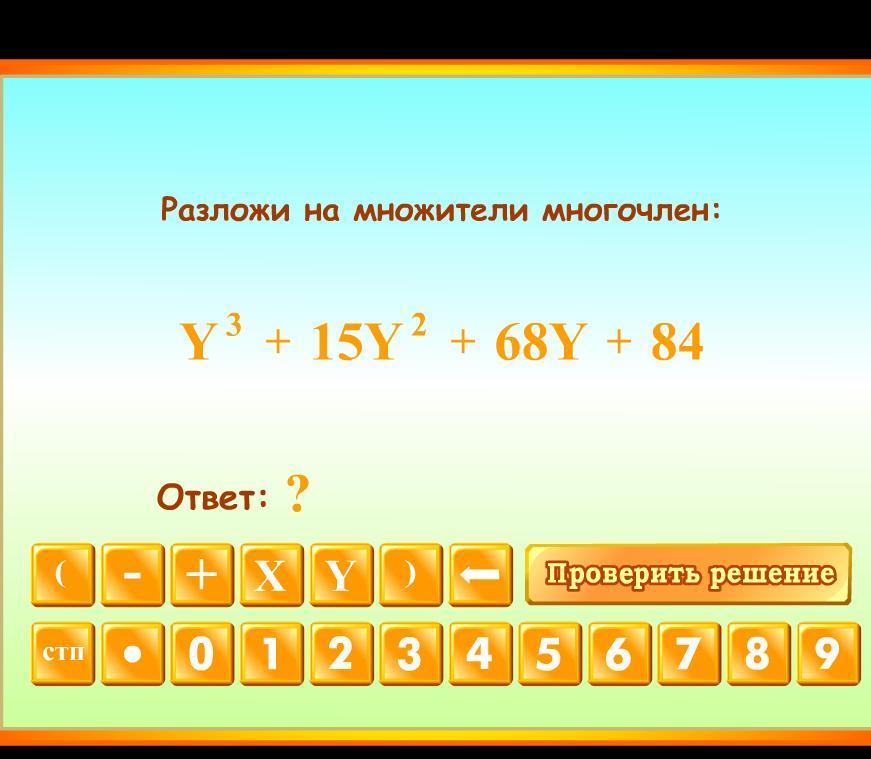
разложи на множители многочлен

Answer 1

Ответ:

      $y^3+15y^2+68y+84$

Подберём один из корней многочлена, являющийся делителем cвободного члена 84.

Это будет число  -2 , так как  

$(-2)^3+15(-2)^2+68(-2)+84=-8+60-136+84=0$ .

Делим многочлен на (х+2), получим

$y^3+15y^2+68y+84=(y+2)(y^2+13y+42)$  

По теореме Виета легко найти корни квадратного трёхчлена

$y^2+13y+42$  . Это числа  -6  и  -7  .  Тогда

  $y^3+15y^2+68y+84=(y+2)(y^2+13y+42)=(y+7)(y+6)(y+2)$