Предмет: Алгебра,
автор: fogyfor123
Розв‘яжіть систему нерівностей)
Прошу пояснень кожної дії
Приложения:
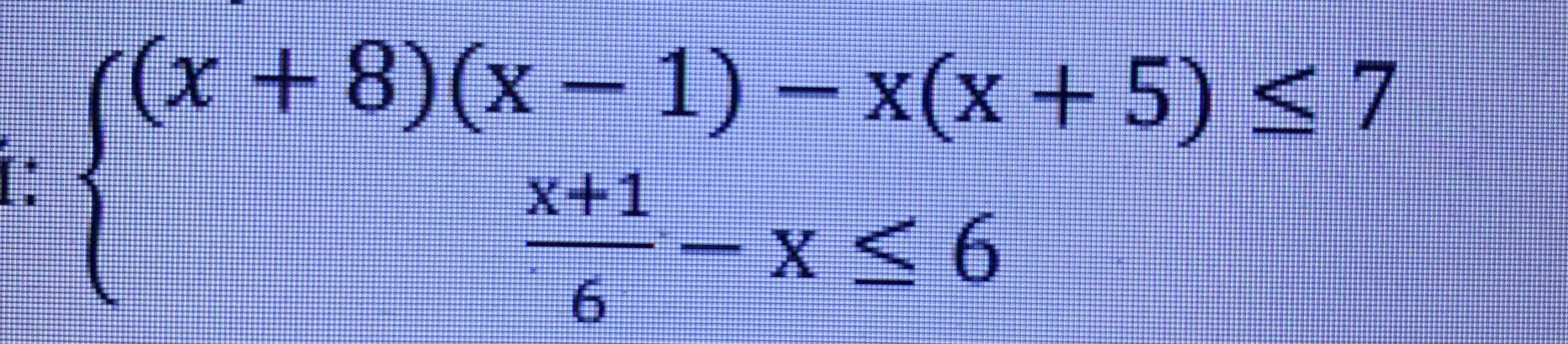
Ответы
Автор ответа:
0
Відповідь:
[-7 ; 7,5]
Пояснення:
Решим оба по отдельности, а потом найдем общие корни:
- 1)
Раскрываем скобки, и сокращаем
х є (-∞ ; 7,5]
- 2)
Умножим на 6 и упростим
Умножим на (-1), помня, что при умножении неравенства на отрицательное значение, знак неравенства меняется в обратною сторону
х є [-7 ; +∞)
- Теперь найдем общие корни для (-∞ ; 7,5] и [-7 ; +∞)
(-∞ ; 7,5] ∩ [-7 ; +∞) = [-7 ; 7,5]
Автор ответа:
0
Похожие вопросы
Предмет: Французский язык,
автор: Alinamilki
Предмет: Русский язык,
автор: ljudmila0008
Предмет: Русский язык,
автор: ТомилаБелошапкина
Предмет: Химия,
автор: Аноним
Предмет: Литература,
автор: mariyatesfaye1723