Решить уравнение для вступительного экзамена по математике

Ответы
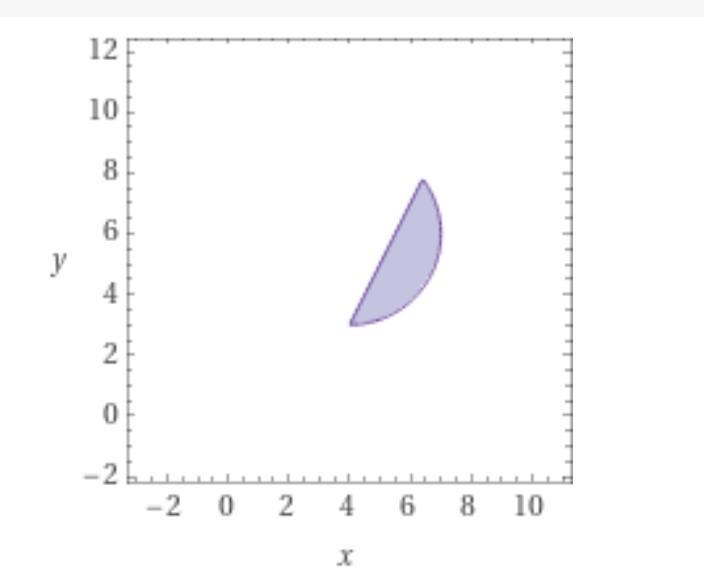
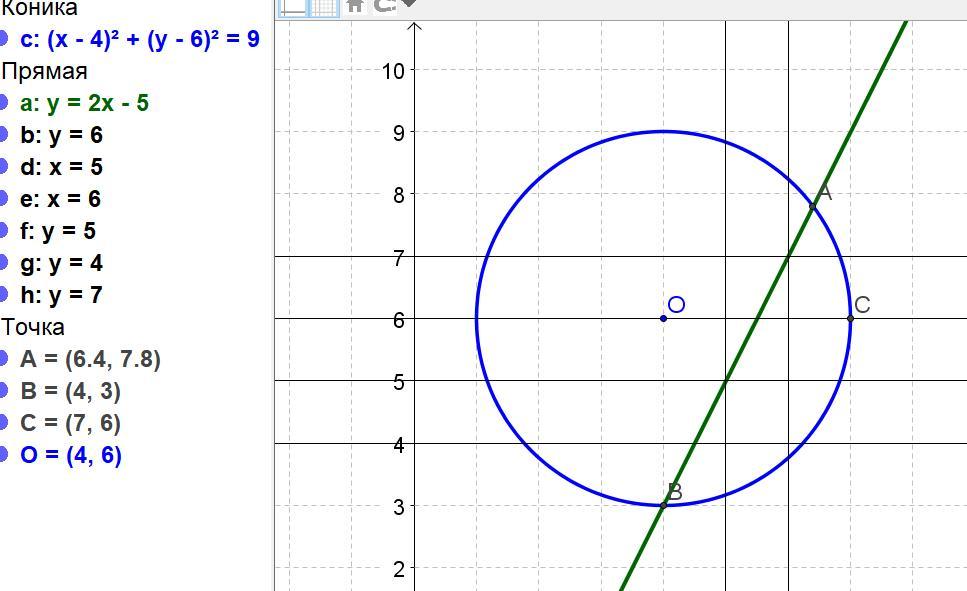
Даны 2 неравенства: x² + y² - 8x - 12y + 43 < 0, y - 2x + 5 < 0.
В первом выделим полные квадраты.
(x² - 2*4x + 16) – 16 + (y² - 2*6y + 36) – 36 + 43 < 0
(x – 4)² + (y – 6)² < 9.
Получили внутреннюю часть окружности радиусом 3 с центром в точке (4; 6).
Второе неравенство даёт часть плоскости, расположенную ниже прямой y = 2x – 5.
Совместное решение даёт часть окружности ниже прямой.
Находим крайние точки.
x²+y²-8x-12y+43=0, y=2x-5,
x²+(2x-5)²-8x-12(2x-5)+43=0,
x²+4x²-20x+25-8x-24x+60+43=0,
5x²-52x+128=0,
D=(-52)^2-4*5*128=2704-4*5*128=2704-20*128=2704-2560=144;
x_1=(2root144-(-52))/(2*5)=(12-(-52))/(2*5)=(12+52)/(2*5)=64/(2*5)=64/10=6,4;
x_2=(-2root144-(-52))/(2*5)=(-12-(-52))/(2*5)=(-12+52)/(2*5)=40/(2*5)=40/10=4.
Значит, крайняя левая точка имеет абсциссу х=4.
Значение ординаты в этой точке: у = 2*4-5 = 3.
Максимальная ордината заданной области принадлежит точке х=6,4.
Тогда у = 2*6,4-5 = 7,8.
Крайняя правая точка заданной области – это точка на окружности на уровне центра (у = 6). Находим: (x – 4)² + (y – 6)² = 9, х-4 = 3, х = 7.
Получаем, что целые числа в заданной области находятся в промежутке:
по оси Ох: (4…7), это числа 5 и 6,
по оси Оу: (3…7,8), это числа 4, 5 и 6. Им соответствуют координаты:
(5; 4), (6; 4), (6; 5), (6; 6). Их сумма равна 9+10+11+12 = 42.
Ответ: сумма равна 42.