Question

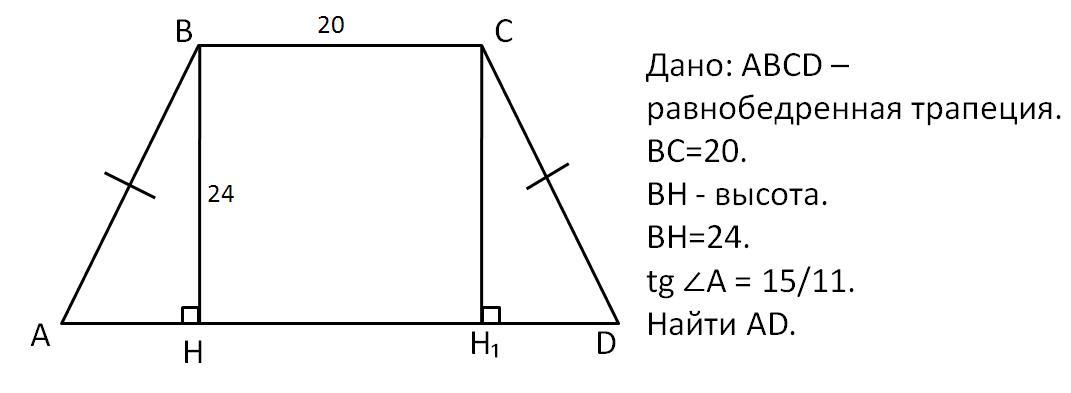
меньшее основание равнобедренной трапеции равно 20 высота трапеции равна 24 Тангенс острого угла равен 15/11 Найдите большее основания​

Answer 1

Меньшее основание равнобедренной трапеции равно 20, высота трапеции равна 24, тангенс острого угла равен 15/11. Найти большее основание.

Ответ:

Большее из двух оснований трапеции равно 55,2(ед.)

Объяснение:

• Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).

Рассмотрим ΔАВН - прямоугольный (ВН - высота ⇒ ВН⊥АD).

$\displaystyle \text{tg}\ \angle A =\frac{BH}{AH}=\frac{15}{11}$

Подставляем значение ВН=24 и находим длину АН:

$\displaystyle \frac{24}{AH}=\frac{15}{11} \Longrightarrow AH=\frac{24\cdot11}{15} =\frac{8*11}{5}= \frac{88}{5}=17.6$

АН = 17.6

• Углы при основаниях/боковые стороны равнобедренной трапеции равны между собою.

ABCD - равнобедренная трапеция ⇒ ∠BAD=∠CDA; АВ=СD.

Проведём высоту CH₁⊥AD.

ΔАВН и ΔСDН₁ - прямоугольные (CH₁⊥AD, АH⊥AD), ∠BAD=∠CDA; АВ=СD ⇒ ΔВАН = ΔСDН₁.

С равенства треугольников ΔВАН и ΔСDН₁ имеем DH₁=AH=17.6.

• Основания трапеции параллельны между собою.

ABCD - трапеция ⇒ AD∥ВС.

• Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой прямой.

AD∥ВС, CH₁⊥AD, АH⊥AD ⇒ CH₁⊥ВС, АH⊥ВС.

CH₁⊥AD, АH⊥AD, CH₁⊥ВС и АH⊥ВС ⇒ ∠CBH=∠BHH₁=∠HH₁C= ∠H₁CB=90°.

Рассмотрим четырёхугольник BHH₁С.

∠CBH=∠BHH₁=∠HH₁C= ∠H₁CB=90°, соответственно четырёхугольник BHH₁С - прямоугольник.

Так как BHH₁С - прямоугольник, HH₁=ВС=20.

AD=HH₁+AH+CH₁=20+17.6+17.6=55,2.